题目内容
对于二次函数y=x2-3x+2和一次函数y=-2x+4,把函数y=t(x2-3x+2)+(1-t)(-2x+4)(t为常数)称为这两个函数的“衍生二次函数”.已知不论t取何常数,这个函数永远经过某些定点,则这个函数必经过的定点坐标为 .
(2,0)、(-1,6).
解析试题分析:将抛物线y展开,然后将含t值的式子整合到一起,令该式子为0(此时无论t取何值都不会对函数值产生影响),即可求出这个定点的坐标;
试题解析:将抛物线y的解析式展开,得:
y=t(x2-3x+2)+(1-t)(-2x+4)=t(x-2)(x+1)-2x+4
∴抛物线E必过定点(2,0)、(-1,6).
考点:二次函数综合题.

练习册系列答案
相关题目
若抛物线 与y轴的交点为(0,﹣3),则下列说法不正确的是【 】
与y轴的交点为(0,﹣3),则下列说法不正确的是【 】
| A.抛物线开口向上 |
| B.抛物线的对称轴是x=1 |
| C.当x=1时,y的最大值为﹣4 |
| D.抛物线与x轴的交点为(-1,0),(3,0) |




 的图像向下平移2个单位后经过点(1,3),那么
的图像向下平移2个单位后经过点(1,3),那么 .
. 的横坐标,将它所对的面的数字作为点
的横坐标,将它所对的面的数字作为点 与
与 轴所围成的区域内(不含边界)的概率是 .
轴所围成的区域内(不含边界)的概率是 . 的解为 。
的解为 。
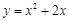 的对称轴是 .
的对称轴是 .