题目内容
小明动手做了一个质地均匀、六个面完全相同的正方体,,分别标有整数-2、-1、0、1、2、3,且每个面和它所相对的面的数字之和均相等,小明向上抛掷该正方体,落地后正方体正面朝上数字作为为点 的横坐标,将它所对的面的数字作为点
的横坐标,将它所对的面的数字作为点 的纵坐标,则点
的纵坐标,则点 落在抛物线
落在抛物线 与
与 轴所围成的区域内(不含边界)的概率是 .
轴所围成的区域内(不含边界)的概率是 .
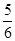 .
.
解析试题分析:由条件分析可以得出P点的坐标共有6中情况:(-1,2)、(-2,3)、(0,1)、(2,-1)、(1,0)、(3,-2),在求出抛物线y=- x2+6与x轴所围成的区域内(不含边界)的是有可能情况,即可得到P落在抛物线内的概率.
x2+6与x轴所围成的区域内(不含边界)的是有可能情况,即可得到P落在抛物线内的概率.
试题解析:∵正方体骰子(每个面的点数分别为-2、-1、0、1、2、3,且相对面的点数和相等,
∴P点的坐标为::(-1,2)、(-2,3)、(0,1)、(2,-1)、(1,0)、(3,-2),
∵y=- x2+6,
x2+6,
令y=0,则x=-2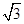 或2
或2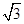 ,
,
∴与x轴所围成的区域内(不含边界)取值范围为:-2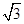 <x<2
<x<2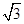 ,
,
∴点P落在抛物线y=- x2+6与x轴所围成的区域内(不含边界)有(-1,2)、(-2,0)、(0,1)、(2,-1)、(0,1),
x2+6与x轴所围成的区域内(不含边界)有(-1,2)、(-2,0)、(0,1)、(2,-1)、(0,1),
点P落在抛物线y=- x2+6与x轴所围成的区域内(不含边界)的概率=
x2+6与x轴所围成的区域内(不含边界)的概率=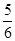 .
.
考点:1.列表法与树状图法;2.二次函数的性质.

练习册系列答案
相关题目
如图,在平面直角坐标系中,抛物线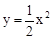 经过平移得到抛物线
经过平移得到抛物线 ,其对称轴与两段抛物线所围成的阴影部分的面积为
,其对称轴与两段抛物线所围成的阴影部分的面积为
| A.2 | B.4 | C.8 | D.16 |
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是
| A.a>0 | B.3是方程ax2+bx+c=0的一个根 |
| C.a+b+c=0 | D.当x<1时,y随x的增大而减小 |

 的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .
的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .
 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
