题目内容
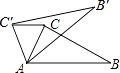
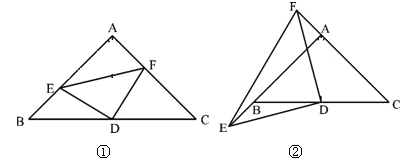
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
(1)如图①,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)如图②,若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;
(2)还是证明:△BED≌△AFD,主要证∠DAF=∠DBE(∠DBE=180°-45°=135°,∠DAF=90°+45°=135°),再结合两组对边对应相等,所以两个三角形全等.
试题解析:(1)连接AD,
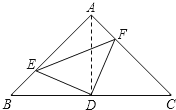
∵AB=AC,∠BAC=90°,D为BC的中点,
∴AD⊥BC,BD=AD.
∴∠B=∠DAC=45°
又BE=AF,
∴△BDE≌△ADF(SAS).
∴ED=FD,∠BDE=∠ADF.
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°.
∴△DEF为等腰直角三角形.
(2)△DEF为等腰直角三角形.理由:
若E,F分别是AB,CA延长线上的点,如图所示:
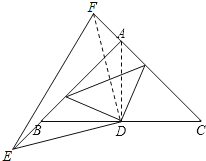
连接AD,
∵AB=AC,
∴△ABC为等腰三角形,
∵∠BAC=90°,D为BC的中点,
∴AD=BD,AD⊥BC(三线合一),
∴∠DAC=∠ABD=45°.
∴∠DAF=∠DBE=135°.
又AF=BE,
∴△DAF≌△DBE(SAS).
∴FD=ED,∠FDA=∠EDB.
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.
∴△DEF仍为等腰直角三角形.

【题目】某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
测试项目 | |||
测试成绩/分 | |||
甲 | 乙 | 丙 | |
教学能力 | 85 | 73 | 73 |
科研能力 | 70 | 71 | 65 |
组织能力 | 64 | 72 | 84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由.