题目内容
菱形ABCD的∠DAB=80°,AB的垂直平分线交对角线AC于F,连DF,则∠CDF=( )
| A、50° | B、40° | C、75° | D、60° |
分析:由菱形ABCD,可得AB=AD,∠DAC=∠BAC=
∠DAB=40°,∠ADC=100°,即可得△ADF≌△ABF,则∠ADF=∠ABF;又因为EF是AB的垂直平分线,所以AF=BF,所以∠ABF=∠BAF=40°,即可求得∠CDF的度数.
| 1 |
| 2 |
解答: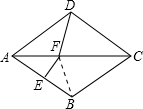 解:∵四边形ABCD是菱形,∠DAB=80°,
解:∵四边形ABCD是菱形,∠DAB=80°,
∴AB=AD,∠DAC=∠BAC=
∠DAB=40°,∠ADC=100°,
∵AF=AF,
∴△ADF≌△ABF,
∴∠ADF=∠ABF;
又∵EF是AB的垂直平分线,
∴AF=BF,
∴∠ABF=∠BAF=40°,
∴∠ADF=40°,
∴∠CDF=∠ADC-∠ADF=60°.
故选D.
 解:∵四边形ABCD是菱形,∠DAB=80°,
解:∵四边形ABCD是菱形,∠DAB=80°,∴AB=AD,∠DAC=∠BAC=
| 1 |
| 2 |
∵AF=AF,
∴△ADF≌△ABF,
∴∠ADF=∠ABF;
又∵EF是AB的垂直平分线,
∴AF=BF,
∴∠ABF=∠BAF=40°,
∴∠ADF=40°,
∴∠CDF=∠ADC-∠ADF=60°.
故选D.
点评:此题考查了菱形的性质:菱形的四条边都相等,对角平分一组对角.还考查了垂直平分线的性质.解题时注意作出适当的辅助线.

练习册系列答案
相关题目
 如图,菱形ABCD的对角线AC和BD相交于O点,E,F,G,H分别是AB,BC,CD,DA的中点,求证:E,F,G,H四个点在以O为圆心的同一个圆上.
如图,菱形ABCD的对角线AC和BD相交于O点,E,F,G,H分别是AB,BC,CD,DA的中点,求证:E,F,G,H四个点在以O为圆心的同一个圆上.
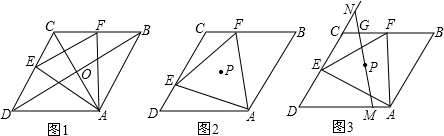
 如图,菱形ABCD的边长为4,点P1在AB边上,且AP1=3.在BC边上截取BP2=AP1,得点P2;在CD边上截取CP3=BP2,得点p3;在DA边上截取DP4=CP3,得点p4;在AB边上截取AP5=DP4,得点P5;…,按此作法进行下去,则点p2011( )
如图,菱形ABCD的边长为4,点P1在AB边上,且AP1=3.在BC边上截取BP2=AP1,得点P2;在CD边上截取CP3=BP2,得点p3;在DA边上截取DP4=CP3,得点p4;在AB边上截取AP5=DP4,得点P5;…,按此作法进行下去,则点p2011( )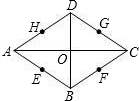 如图,菱形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是它的四条边AB、BC、CD、DA的中点,E、F、G、H四个点共圆吗?(友情提示:要找到一点,证明这四点到找到的这点(圆心)的距离相等即可)
如图,菱形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是它的四条边AB、BC、CD、DA的中点,E、F、G、H四个点共圆吗?(友情提示:要找到一点,证明这四点到找到的这点(圆心)的距离相等即可)