��Ŀ����
��֪����ABCD�ı߳�Ϊ1����ADC=60�㣬�ȱߡ�AEF���߷ֱ�DC��CB�ڵ�E��F��
��1�����ⷢ�֣���ͼ1������E��F�ֱ��DZ�DC��CB���е㣬��֤������ABCD�Խ���AC��BD�Ľ���O��Ϊ�ȱߡ�AEF�����ģ�
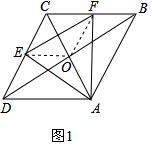
��2������E��Fʼ�շֱ��ڱ�DC��CB���ƶ����ǵȱߡ�AEF������ΪP�� �ٲ�����֤����ͼ2�������AEF������P������һֱ���ϣ�������֤��������չ���ã���ͼ3����E��F�ֱ��DZ�DC��CB���е�ʱ������P����һֱ�ߣ��ֱ�DA���ڵ�M��BC���ڵ�G��DC�ߵ��ӳ����ڵ�N������ֱ��д��
+
��ֵ��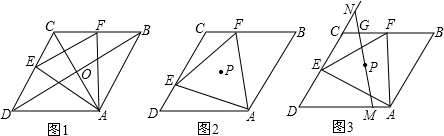
��1�����ⷢ�֣���ͼ1������E��F�ֱ��DZ�DC��CB���е㣬��֤������ABCD�Խ���AC��BD�Ľ���O��Ϊ�ȱߡ�AEF�����ģ�
��2������E��Fʼ�շֱ��ڱ�DC��CB���ƶ����ǵȱߡ�AEF������ΪP�� �ٲ�����֤����ͼ2�������AEF������P������һֱ���ϣ�������֤��������չ���ã���ͼ3����E��F�ֱ��DZ�DC��CB���е�ʱ������P����һֱ�ߣ��ֱ�DA���ڵ�M��BC���ڵ�G��DC�ߵ��ӳ����ڵ�N������ֱ��д��
| 1 |
| DM |
| 1 |
| DN |

��������1������OE��0F�����ı���ABCD�����Σ��ó�AC��BD��BDƽ�֡�ADC��AD=DC=BC������E��F�ֱ�ΪDC��CB�е㣬֤��0E=OF=OA����ɵõ�O��Ϊ��AEF�����ģ�
��2��������PE��PA������P�ֱ���PI��CD��I��PJ��AD��J�������IPJ�Ķ��������ɵ�P�ǵȱߡ�AEF�����ģ���֤�á�PIE�ա�PJA���ɵ�PI=PJ������P�ڡ�ADC��ƽ�����ϣ�����P����ֱ��DB�ϣ�
������BD��AC���ڵ�P���ɣ�1���ɵõ�P��Ϊ��AEF�����ģ���DM=x��DN=y��x��0��y��O������CN=y-1��������AAS֤����GBP�ա�MDP���ó�BG=DM=x��CG=1-x������BC��DA���ó���NCG�ס�NDM���������������ζ�Ӧ�߳ɱ����ó�
=
���������
+
Ϊ��ֵ2��
��2��������PE��PA������P�ֱ���PI��CD��I��PJ��AD��J�������IPJ�Ķ��������ɵ�P�ǵȱߡ�AEF�����ģ���֤�á�PIE�ա�PJA���ɵ�PI=PJ������P�ڡ�ADC��ƽ�����ϣ�����P����ֱ��DB�ϣ�
������BD��AC���ڵ�P���ɣ�1���ɵõ�P��Ϊ��AEF�����ģ���DM=x��DN=y��x��0��y��O������CN=y-1��������AAS֤����GBP�ա�MDP���ó�BG=DM=x��CG=1-x������BC��DA���ó���NCG�ס�NDM���������������ζ�Ӧ�߳ɱ����ó�
| CN |
| DN |
| CG |
| DM |
| 1 |
| DM |
| 1 |
| DN |
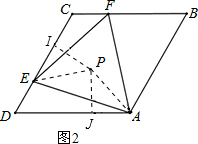
��� ��1��֤������ͼ1������OE��0F��
��1��֤������ͼ1������OE��0F��
���ı���ABCD�����Σ�
��AC��BD��BDƽ�֡�ADC��AD=DC=BC��
���COD=��COB=��AOD=90�㣮
��ADO=
��ADC=
��60��=30�㣬
�֡�E��F�ֱ�ΪDC��CB�е㣬
��OE=
CD��OF=
BC��AO=
AD��
��0E=OF=OA��
���O��Ϊ��AEF�����ģ�
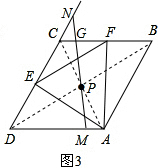
 ��2���⣺�ٲ��룺����Pһ������ֱ��DB�ϣ��������£�
��2���⣺�ٲ��룺����Pһ������ֱ��DB�ϣ��������£�
��ͼ2���ֱ�����PE��PA������P�ֱ���PI��CD��I��PJ��AD��J��
���PIE=��PJD=90�㣬
�ߡ�ADC=60�㣬
���IPJ=360��-��PIE-��PJD-��JDI=120�㣬
�ߵ�P�ǵȱߡ�AEF�����ģ�
���EPA=120�㣬PE=PA��
���IPJ=��EPA��
���IPE=��JPA��
���PIE�ա�PJA��
��PI=PJ��
���P�ڡ�ADC��ƽ�����ϣ�����P����ֱ��DB�ϣ�
��
+
Ϊ��ֵ2��
 ����BD��AC���ڵ�P���ɣ�1���ɵõ�P��Ϊ��AEF�����ģ�
����BD��AC���ڵ�P���ɣ�1���ɵõ�P��Ϊ��AEF�����ģ�
��ͼ3����MN��BC�ڵ�G��
��DM=x��DN=y��x��0��y��O������CN=y-1��
��BC��DA��
���GBP=��MDP����BGP=��DMP��
���ɣ�1��֪BP=DP��
���GBP�ա�MDP��AAS����
��BG=DM=x��
��CG=1-x��
��BC��DA��
���NCG�ס�NDM��
��
=
��
��
=
��
��x+y=2xy��
��
+
=2��
��
+
=2��
 ��1��֤������ͼ1������OE��0F��
��1��֤������ͼ1������OE��0F�����ı���ABCD�����Σ�
��AC��BD��BDƽ�֡�ADC��AD=DC=BC��
���COD=��COB=��AOD=90�㣮
��ADO=
| 1 |
| 2 |
| 1 |
| 2 |
�֡�E��F�ֱ�ΪDC��CB�е㣬
��OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��0E=OF=OA��
���O��Ϊ��AEF�����ģ�
 ��2���⣺�ٲ��룺����Pһ������ֱ��DB�ϣ��������£�
��2���⣺�ٲ��룺����Pһ������ֱ��DB�ϣ��������£���ͼ2���ֱ�����PE��PA������P�ֱ���PI��CD��I��PJ��AD��J��
���PIE=��PJD=90�㣬
�ߡ�ADC=60�㣬
���IPJ=360��-��PIE-��PJD-��JDI=120�㣬
�ߵ�P�ǵȱߡ�AEF�����ģ�
���EPA=120�㣬PE=PA��
���IPJ=��EPA��
���IPE=��JPA��
���PIE�ա�PJA��
��PI=PJ��
���P�ڡ�ADC��ƽ�����ϣ�����P����ֱ��DB�ϣ�
��
| 1 |
| DM |
| 1 |
| DN |
 ����BD��AC���ڵ�P���ɣ�1���ɵõ�P��Ϊ��AEF�����ģ�
����BD��AC���ڵ�P���ɣ�1���ɵõ�P��Ϊ��AEF�����ģ���ͼ3����MN��BC�ڵ�G��
��DM=x��DN=y��x��0��y��O������CN=y-1��
��BC��DA��
���GBP=��MDP����BGP=��DMP��
���ɣ�1��֪BP=DP��
���GBP�ա�MDP��AAS����
��BG=DM=x��
��CG=1-x��
��BC��DA��
���NCG�ס�NDM��
��
| CN |
| DN |
| CG |
| DM |
��
| y-1 |
| y |
| 1-x |
| x |
��x+y=2xy��
��
| 1 |
| x |
| 1 |
| y |
��
| 1 |
| DM |
| 1 |
| DN |
���������⿼����ȫ�������Ρ����������ε��ж������ʣ������ε����ĵ��ж������ʣ����ε����ʵ�֪ʶ�������ۺ��Ժ�ǿ��ͼ��Ҳ�Ƚϸ��ӣ�����Ĺؼ��Ƿ���˼�������ν��˼���Ӧ�ã�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
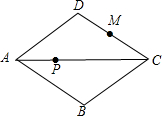 ��ͼ����֪����ABCD�ı߳�Ϊ6����һ�ڽ�Ϊ60�㣬MΪCD���ϵ��е㣬PΪ�Խ���AC�ϵĶ��㣬��PD+PM����СֵΪ
��ͼ����֪����ABCD�ı߳�Ϊ6����һ�ڽ�Ϊ60�㣬MΪCD���ϵ��е㣬PΪ�Խ���AC�ϵĶ��㣬��PD+PM����СֵΪ �����
����� ��ͼ����֪����ABCD�ı�AB=2cm�������ܳ�Ϊ
��ͼ����֪����ABCD�ı�AB=2cm�������ܳ�Ϊ