题目内容
(本题满分10分)如图,将OA = 6,AB = 4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.

(1)点B的坐标为 ;用含t的式子表示点P的坐标为 ;(3分)
(2)记△OMP的面积为S,求S与t的函数关系式(0 < t < 6);并求t为何值时,S有最大值?(4分)
(3)试探究:当S有最大值时,在y轴上是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC面积的
 ?若存在,求出点T的坐标;若不存在,请说明理由.(3分)
?若存在,求出点T的坐标;若不存在,请说明理由.(3分)
(1)(6,4);(
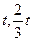 )
)(2)当
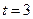 时,S有最大值
时,S有最大值(3)存在,在y轴上存在点T1(0,
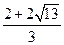 ),T2(0,
),T2(0,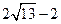 )符合条件解析:
)符合条件解析:解:(1)(6,4);(
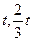 ).(其中写对B点得1分) 3分
).(其中写对B点得1分) 3分(2)∵S△OMP =
 ×OM×
×OM× , 4分
, 4分∴S =
 ×(6 -t)×
×(6 -t)× =
=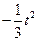 +2t.
+2t.=
 (0 < t <6). 6分
(0 < t <6). 6分∴当
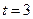 时,S有最大值. 7分
时,S有最大值. 7分(3)存在.
由(2)得:当S有最大值时,点M、N的坐标分别为:M(3,0),N(3,4),
则直线ON的函数关系式为:
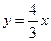 .
.设点T的坐标为(0,b),则直线MT的函数关系式为:
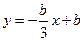 ,
,解方程组
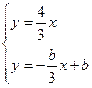 得
得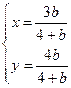
∴直线ON与MT的交点R的坐标为
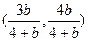 .
.∵S△OCN =
 ×4×3=6,∴S△ORT =
×4×3=6,∴S△ORT = S△OCN =2. 8分
S△OCN =2. 8分当点T在点O、C之间时,分割出的三角形是△OR1T1,如图,作R1D1⊥y轴,D1为垂足,则S△OR1T1=
 ••••RD1•OT =
••••RD1•OT = •
•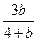 •b=2.
•b=2.
∴
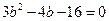 , b =
, b = .
.∴b1 =
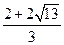 ,b2 =
,b2 =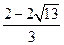 (不合题意,舍去)
(不合题意,舍去)此时点T1的坐标为(0,
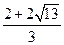 ). 9分
). 9分② 当点T在OC的延长线上时,分割出的三角形是△R2NE,如图,设MT交CN于点E,由①得点E的横坐标为
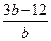 ,作R2D2⊥CN交CN于点D2,则
,作R2D2⊥CN交CN于点D2,则S△R2NE=
 •EN•R2D2 =
•EN•R2D2 = •
•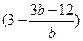 •
•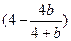
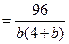 =2.
=2.∴
 ,b=
,b= .
.∴b1=
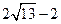 ,b2=
,b2= (不合题意,舍去).
(不合题意,舍去).∴此时点T2的坐标为(0,
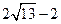 ).
).综上所述,在y轴上存在点T1(0,
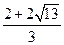 ),T2(0,
),T2(0,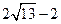 )符合条件.…10分
)符合条件.…10分 
练习册系列答案
相关题目

 的图象的顶点为
的图象的顶点为 .二次函数
.二次函数 的图象与
的图象与 轴交于原点
轴交于原点 及另一点
及另一点 ,它的顶点
,它的顶点 在函数
在函数
 为菱形时,求函数
为菱形时,求函数 与支架
与支架 所在直线相交于水箱横断面
所在直线相交于水箱横断面 的圆心
的圆心 ,支架
,支架 垂直,
垂直, 厘米,
厘米,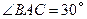 ,另一根辅助支架
,另一根辅助支架 厘米,
厘米, .
. 的长度.(结果保留三个有效数字,参考数据:
的长度.(结果保留三个有效数字,参考数据: )
)


