Question

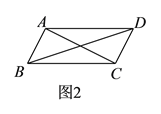
【题目】如图，正方形ABCD中，AB=4，E为BC的中点，F为AE的中点，过点F作GH⊥AE，分别交AB和CD于G，H，求GF的长，并求 的值．

Answer 1

【答案】解：作GM⊥BC垂足为M，
∵四边形ABCD是正方形，
∴AD=CD=AB=BC=4，∠ADC=∠=90°，
在RtABE中，∵DE=DC=2，AD=4
∴AE= =2 ，
∵AF=EF，
∴AF= ，
∵∠FAG=∠DAE，∠AFG=∠ADE=90°
∴△AFG∽△ADE
得 = ，
∴ ，
∴GF= ，
∵∠GDC=∠D=∠DCM=∠CMD=90°，
∴四边形GMCD是矩形，
∴GM=CD=AD，∠MGD=90°，
∴∠HGM+∠AGF=90°，∠AGF+∠DAE=90°，
∴∠DAE=∠GHM，
在△ADE和△GMH中，
，
∴△ADE≌△GMH，
∴HG=AE=2 ，FH=GH﹣FG= ，
∴ = ．

【解析】先在RT△ADE中求出AE，再利用△AFG∽△ADE得 = ，即可求出FG，再利用△ADE≌△GMH证明AE=GH即可求出FH即可解决问题．
【考点精析】利用勾股定理的概念和正方形的性质对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．