题目内容
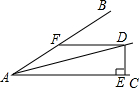
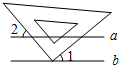
如图,AB∥EF,在AB、EF之间,且在BF的左侧任意选取一点C,试猜想∠B、∠F、∠C之间的关系,试加以说明.


∠BCF=∠B+∠F.
理由:过点C作CD∥EF,
∵CD∥EF,
∴∠F=∠1(两直线平行,内错角相等),
∵AB∥EF,EF∥CD,
∴AB∥CD(同平行于一直线的两直线平行),
∴∠B=∠2(两直线平行,内错角相等),
又∵∠BCF=∠1+∠2,
∴∠BCF=∠B+∠F.
理由:过点C作CD∥EF,
∵CD∥EF,
∴∠F=∠1(两直线平行,内错角相等),
∵AB∥EF,EF∥CD,
∴AB∥CD(同平行于一直线的两直线平行),
∴∠B=∠2(两直线平行,内错角相等),
又∵∠BCF=∠1+∠2,
∴∠BCF=∠B+∠F.

练习册系列答案
相关题目