题目内容
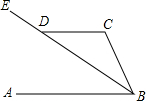
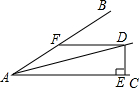
如图所示,∠BAC=30°,D为角平分线上一点,DE⊥AC于E,DF∥AC,且交AB于点F.
(1)求∠ADE的度数;
(2)试判断△AFD的形状,并说明理由.
(1)求∠ADE的度数;
(2)试判断△AFD的形状,并说明理由.

(1)∵∠BAC=30°,AD为∠BAC的角平分线,DE⊥AC,
∴∠BAD=∠CAD=
×30°=15°.
在△ADE中,∠ADE=180°-15°-90°=75°.
(2)∵AD为∠BAC的角平分线,
∴∠FAD=∠DAE.
∵DF∥AC,
∴∠ADF=∠DAE.
故∠FAD=∠ADF.
△AFD是等腰三角形.
∴∠BAD=∠CAD=
| 1 |
| 2 |
在△ADE中,∠ADE=180°-15°-90°=75°.
(2)∵AD为∠BAC的角平分线,
∴∠FAD=∠DAE.
∵DF∥AC,
∴∠ADF=∠DAE.
故∠FAD=∠ADF.
△AFD是等腰三角形.

练习册系列答案
相关题目