题目内容
设a、b是实数,且
-
=
,求
+
的值.
| 1 |
| 1+a |
| 1 |
| 1+b |
| 1 |
| b-a |
| 1+b |
| 1+a |
| 1+a |
| 1+b |
考点:分式的化简求值
专题:计算题
分析:先根据分式混合运算的法则把
-
=
化简为(b-a)2=(1+a)(1+b),再把所求代数式进行化简,把(b-a)2=(1+a)(1+b)代入进行计算即可.
| 1 |
| 1+a |
| 1 |
| 1+b |
| 1 |
| b-a |
解答:解:∵
-
=
,
∴
=
,即
=
,
∴(b-a)2=(1+a)(1+b),
∴原式=
+
=
=
=
=
=3.
| 1 |
| 1+a |
| 1 |
| 1+b |
| 1 |
| b-a |
∴
| 1+b-1-a |
| (1+a)(1+b) |
| 1 |
| b-a |
| b-a |
| (1+a)(1+b) |
| 1 |
| b-a |
∴(b-a)2=(1+a)(1+b),
∴原式=
| 1+b |
| 1+a |
| 1+a |
| 1+b |
=
| (1+b)2+(1+a)2 |
| (1+a)(1+b) |
=
| [(1+a)2-(1+b)]2+2(1+a)(1+b) |
| (1+a)(1+b) |
=
| (b-a)2+2(1+a)(1+b) |
| (1+a)(1+b) |
=
| 3(b-a)2 |
| (b-a)2 |
=3.
点评:本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
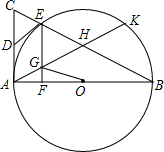 在Rt△ABC中,∠BAC=90°,以AB为直径⊙O交BC于点E,D为AC中点,EF⊥AB于点F.过A作AK∥DE交⊙O于K,交BC于H,交EF于G.
在Rt△ABC中,∠BAC=90°,以AB为直径⊙O交BC于点E,D为AC中点,EF⊥AB于点F.过A作AK∥DE交⊙O于K,交BC于H,交EF于G.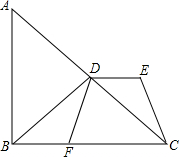 在Rt△ABC中,BD是斜边AC的中线,DE∥BF,且DE=BF,试判定四边形DECF的形状.
在Rt△ABC中,BD是斜边AC的中线,DE∥BF,且DE=BF,试判定四边形DECF的形状.