题目内容
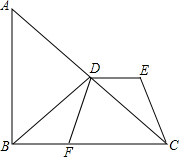 在Rt△ABC中,BD是斜边AC的中线,DE∥BF,且DE=BF,试判定四边形DECF的形状.
在Rt△ABC中,BD是斜边AC的中线,DE∥BF,且DE=BF,试判定四边形DECF的形状.考点:全等三角形的判定与性质,直角三角形斜边上的中线,等腰梯形的判定
专题:几何图形问题
分析:由直角三角形的性质就可以得出BD=CD,∠DBC=∠DCB,由DE∥BC就可以得出∠EDC=∠BCA,就可以得出∠DBC=∠CDE,证明△BDF≌△DCE就可以得出FD=EC,就可以得出四边形DECF为等腰梯形.
解答:解:四边形DECF为等腰梯形
理由:∵△ABC为直角三角形,BD是斜边AC的中线,
∴BD=CD=
AC.
∴∠DBC=∠DCB.
∵DE∥BC,
∴∠EDC=∠BCA,
∴∠DBC=∠CDE.
在△BDF和△DCE中,
,
∴△BDF≌△DCE(SAS),
∴FD=EC.
∵DE∥BF,
∴四边形DECF为等腰梯形.
理由:∵△ABC为直角三角形,BD是斜边AC的中线,
∴BD=CD=
| 1 |
| 2 |
∴∠DBC=∠DCB.
∵DE∥BC,
∴∠EDC=∠BCA,
∴∠DBC=∠CDE.
在△BDF和△DCE中,
|
∴△BDF≌△DCE(SAS),
∴FD=EC.
∵DE∥BF,
∴四边形DECF为等腰梯形.
点评:本题考查了直角三角形的性质的运用,平行线的性质的运用,全等三角形的判定及性质的运用,等腰梯形的判定的运用,解答时证明三角形全等是关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
 一个山坡的倾斜角为10°,坡上有一棵树AB,当阳光与水平线成50°角时,树影BC的长为6米,求树高AB.
一个山坡的倾斜角为10°,坡上有一棵树AB,当阳光与水平线成50°角时,树影BC的长为6米,求树高AB. 如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,求△OCD的周长.
如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,求△OCD的周长. 如图,在△ABC中,cosB=
如图,在△ABC中,cosB=