题目内容
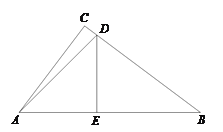
【题目】如图,![]() 是正方形
是正方形![]() 的对角线,
的对角线,![]() .边
.边![]() 在其所在的直线上平移,将通过平移得到的线段记为
在其所在的直线上平移,将通过平移得到的线段记为![]() ,连接
,连接![]() 、
、![]() ,并过点
,并过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]() .
.
(1)请直接写出线段![]() 在平移过程中,四边形
在平移过程中,四边形![]() 是什么四边形;
是什么四边形;
(2)请判断![]() 、
、![]() 之间的数量关系和位置关系,并加以证明;
之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
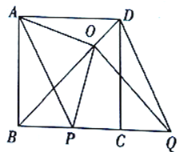
【答案】(1)四边形![]() 是平行四边形;(2)
是平行四边形;(2)![]() 且
且![]() ,证明见解析;(3)见解析.
,证明见解析;(3)见解析.
【解析】
(1)根据平移的性质,可得PQ=BC=AD,根据一组对边平行且相等的四边形是平行四边形,可得答案;
(2)根据正方形的性质,平移的性质,可得PQ与AB的关系,根据等腰直角三角形的判定与性质,可得∠PQO,根据全等三角形的判定与性质,可得AO与OP的数量关系,根据余角的性质,可得AO与OP的位置关系;
(3)根据等腰直角三角形的性质,可得OE的长,根据三角形的面积公式,可得函数关系式.
(1)根据平移的性质可得,PQ=BC,
∵四边形ABCD是正方形,
∴BC=AD,BC∥AD,
∴PQ=AD,PQ∥AD,
∴四边形![]() 是平行四边形.
是平行四边形.
(2)![]() 且
且![]() .证明如下:
.证明如下:
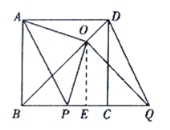
①当![]() 向右平移时,如图,
向右平移时,如图,
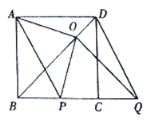
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]() ,
,
∴![]() 且
且![]() .
.
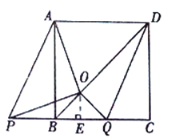
②当![]() 向左平移时,如图,
向左平移时,如图,
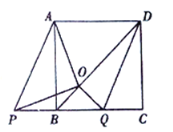
同理可证,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 且
且![]() .
.
(3)过点![]() 作
作![]() 于
于![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
①当![]() 向右平移时,如图,
向右平移时,如图,
![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
②当![]() 向左平移时,如图,
向左平移时,如图,
![]() ,
,
∴![]() .
.
∵![]() .
.
∴![]() .
.

【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 | 面试 | 笔试 | ||
形体 | 口才 | 专业水平 | 创新能力 | |
甲 | 86 | 90 | 96 | 92 |
乙 | 92 | 88 | 95 | 93 |
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照4:6:5:5的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
【题目】自1993年起,联合国将每年的3月22日定为“世界水日”,宗旨是唤起公众的节水意识,加强水资源保护.某校在开展“节约每一滴水”的活动中,从初三年级随机选出20名学生统计出各自家庭一个月的节约用水量,有关数据整理如下表.
节约用水量(单位:吨) | 1 | 1.2 | 1.4 | 2 | 2.5 |
家庭数 | 4 | 6 | 5 | 3 | 2 |
这组数据的中位数和众数分别是( )
A. 1.2,1.2; B. 1.4,1.2; C. 1.3,1.4; D. 1.3,1.2.