题目内容
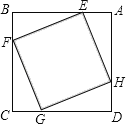
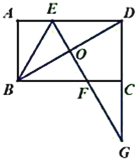
【题目】如图，在菱形ABCD中，tan∠A＝
，M，N分别在AD，BC上，将四边形AMNB沿MN翻折，使AB的对应线段EF经过顶点D，当EF⊥AD时，
的值为_____．
【答案】
．
【解析】
首先延长NF与DC交于点H，进而利用翻折变换的性质得出NH⊥DC，再利用边角关系得出DF，CN的长，进而得出答案．
解：如图，延长NF与DC交于点H，
∵∠ADF＝90°，
∴∠A+∠FDH＝90°，
∵∠DFN+∠DFH＝180°，∠A+∠B＝180°，∠B＝∠DFN，
∴∠A＝∠DFH，
∴∠FDH+∠DFH＝90°，
∴NH⊥DC，
∵tan∠A＝
，由翻折性质可得∠A=∠E，AM=EM，
∴tan∠E=，
在Rt△DME中，可设DM＝4k，DE＝3k，
∴EM＝
5k，
∴AD＝9k＝DC，DF＝6k，
∵tan∠A＝tan∠DFH＝
，
则sin∠DFH＝
，
∴DH＝DF＝
k，
∴CH＝9k﹣k＝
k，
∵cos∠C＝cos∠A＝
＝
，
∴CN＝
CH＝7k，
∴
＝．
故答案为：．
练习册系列答案
相关题目
