题目内容
【题目】现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同．
（1）求该快递公司投递总件数的月平均增长率；
（2）如果平均每人每月最多可投递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？
【答案】（1）10%；（2）2名业务员．
【解析】
试题分析：（1）设该快递公司投递总件数的月平均增长率为x，根据“今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同”建立方程，解方程即可；
（2）首先求出今年6月份的快递投递任务，再求出21名快递投递业务员能完成的快递投递任务，比较得出该公司不能完成今年6月份的快递投递任务，进而求出至少需要增加业务员的人数．
解：（1）设该快递公司投递总件数的月平均增长率为x，根据题意得
10（1+x）2=12.1，
解得x1=0.1，x2=﹣2.2（不合题意舍去）．
答：该快递公司投递总件数的月平均增长率为10%；
（2）今年6月份的快递投递任务是12.1×（1+10%）=13.31（万件）．
∵平均每人每月最多可投递0.6万件，
∴21名快递投递业务员能完成的快递投递任务是：0.6×21=12.6＜13.31，
∴该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务
∴需要增加业务员（13.31﹣12.6）÷0.6=1
≈2（人）．
答：该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务，至少需要增加2名业务员．
高中必刷题系列答案
【题目】如图，李老师设计了一个探究杠杆平衡条件的实验：在一个自制类似天平的仪器的左边固定托盘A中放置一个重物，在右边活动托盘B（可左右移动）中放置一定质量的砝码，使得仪器左右平衡．改变活动托盘B与点O的距离x（cm），观察活动托盘B中砝码的质量y（g）的变化情况．实验数据记录如下表：
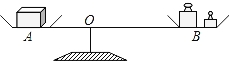
x（cm） | 10 | 15 | 20 | 25 | 30 |
y（g） | 30 | 20 | 15 | 12 | 10 |
（1）猜测y与x之间的函数关系，求出函数关系式并加以验证；
（2）当砝码的质量为24g时，活动托盘B与点O的距离是多少？
（3）将活动托盘B往左移动时，应往活动托盘B中添加还是减少砝码？
