题目内容
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
【答案】
(1)
解:设抛物线解析式为y=ax2+bx+c,
把A、B、C三点坐标代入可得 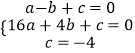 ,解得
,解得 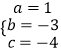 ,
,
∴抛物线解析式为y=x2﹣3x﹣4;
(2)
解:作OC的垂直平分线DP,交OC于点D,交BC下方抛物线于点P,如图1,
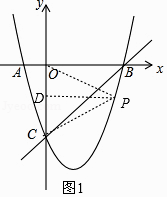
∴PO=PD,此时P点即为满足条件的点,
∵C(0,﹣4),
∴D(0,﹣2),
∴P点纵坐标为﹣2,
代入抛物线解析式可得x2﹣3x﹣4=﹣2,解得x= ![]() (小于0,舍去)或x=
(小于0,舍去)或x= ![]() ,
,
∴存在满足条件的P点,其坐标为( ![]() ,﹣2);
,﹣2);
(3)
解:∵点P在抛物线上,
∴可设P(t,t2﹣3t﹣4),
过P作PE⊥x轴于点E,交直线BC于点F,如图2,
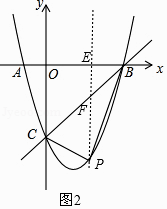
∵B(4,0),C(0,﹣4),
∴直线BC解析式为y=x﹣4,
∴F(t,t﹣4),
∴PF=(t﹣4)﹣(t2﹣3t﹣4)=﹣t2+4t,
∴S△PBC=S△PFC+S△PFB= ![]() PFOE+
PFOE+ ![]() PFBE=
PFBE= ![]() PF(OE+BE)=
PF(OE+BE)= ![]() PFOB=
PFOB= ![]() (﹣t2+4t)×4=﹣2(t﹣2)2+8,
(﹣t2+4t)×4=﹣2(t﹣2)2+8,
∴当t=2时,S△PBC最大值为8,此时t2﹣3t﹣4=﹣6,
∴当P点坐标为(2,﹣6)时,△PBC的最大面积为8.
【解析】(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;(2)由题意可知点P在线段OC的垂直平分线上,则可求得P点纵坐标,代入抛物线解析式可求得P点坐标;(3)过P作PE⊥x轴,交x轴于点E,交直线BC于点F,用P点坐标可表示出PF的长,则可表示出△PBC的面积,利用二次函数的性质可求得△PBC面积的最大值及P点的坐标.

 阅读快车系列答案
阅读快车系列答案
