题目内容
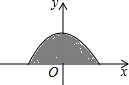 如图所示的阴影部分是抛物线
如图所示的阴影部分是抛物线 在x轴上的部分与x轴所围而成,现将背面完全相同,正面分别标有数-2、-1、
在x轴上的部分与x轴所围而成,现将背面完全相同,正面分别标有数-2、-1、 、
、 、1、2的6张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P横坐标,将该数的相反数作为点p的纵坐标,则点P落在该阴影部分内部的概率为________.
、1、2的6张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P横坐标,将该数的相反数作为点p的纵坐标,则点P落在该阴影部分内部的概率为________.

分析:首先根据题意求得所有点的坐标,由阴影部分是抛物线
 在x轴上的部分与x轴所围而成,可得∴(
在x轴上的部分与x轴所围而成,可得∴( ,-
,- ),(1,-1),(2,-2)不在阴影部分内部,然后分析剩余3个点即可求得答案.
),(1,-1),(2,-2)不在阴影部分内部,然后分析剩余3个点即可求得答案.解答:所有的点为:(-2,2),(-1,1),(-
 ,
, ),(
),( ,-
,- ),(1,-1),(2,-2),
),(1,-1),(2,-2),∵阴影部分在x轴上方,
∴(
 ,-
,- ),(1,-1),(2,-2)不在阴影部分内部,
),(1,-1),(2,-2)不在阴影部分内部,∵当x=-2时,y=-
 ×(-2)2+2=0,
×(-2)2+2=0,又∵2>0,
∴点(-2,2)不在阴影部分内部;
∵当x=-1时,y=-
 ×(-1)2+2=
×(-1)2+2= ,
,又∵1<
 ,
,∴点(-1,1)在阴影部分内部;
∵当x=-
 时,y=-
时,y=- ×(-
×(- )2+2=
)2+2=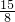 ,
,又∵
 <
<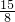 ,
,∴点(-
 ,
, )在阴影部分内部.
)在阴影部分内部.∴一共有2个点在阴影部分内部,
∴点P落在该阴影部分内部的概率为:
 =
= .
.故答案为:
 .
.点评:此题考查了抛物线中点与抛物线的关系与古典概率的知识.题目综合性较强,解题时要注意数形结合思想的应用.

练习册系列答案
相关题目
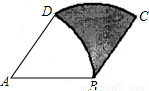
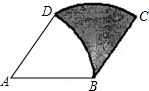 如图所示的阴影部分是某种商品的商标图案.己知菱形ABCD边长是4cm,∠A=60°,弧BD是以A为圆心,AB为半径的弧,弧CD是以B为圆心,BC为半径的弧,则该商标图案的面积是
如图所示的阴影部分是某种商品的商标图案.己知菱形ABCD边长是4cm,∠A=60°,弧BD是以A为圆心,AB为半径的弧,弧CD是以B为圆心,BC为半径的弧,则该商标图案的面积是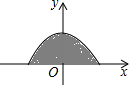 如图所示的阴影部分是抛物线
如图所示的阴影部分是抛物线