题目内容
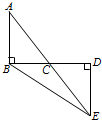
 如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.分析:首先根据垂直可得∠ABC=∠D=90°,再有条件∠ACB=∠DCE,CB=CD,可以用ASA证明△ABC≌△EDC,再根据全等三角形对应边相等得到结论AB=DE.
解答:证明:∵AB⊥BD,ED⊥BD,
∴∠ABC=∠D=90°,
在△ABC和△EDC中
,
∴△ABC≌△EDC(ASA)
∴AB=DE.
∴∠ABC=∠D=90°,
在△ABC和△EDC中
|
∴△ABC≌△EDC(ASA)
∴AB=DE.
点评:此题主要考查了全等三角形的判定与性质,解决此题的关键是找出能使△ABC≌△EDC的条件.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
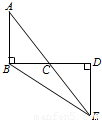
 (1)如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
(1)如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.