题目内容
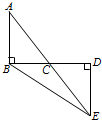
如图,AB⊥BD于点B,ED⊥BD于点D,AB=CD,BC=DE,则∠ACE=_______.

【答案】
90°.
【解析】
试题分析:∵AB⊥BD于点B,ED⊥BD于点D,AB=CD,BC=DE,∴Rt△ABC≌Rt△CDE(HL).
∴∠A=∠DCE,∠ACB=∠E(全等三角形对应边相等).
由AB⊥BD于点B可得∠A+∠ACB=90°(直角三角形两锐角互余).
∴∠ACE=180°-(∠ACB+∠DCE)=180°-(∠ACB+∠A)=90°(等量代换).
考点: 1.全等三角形的判定和性质;2.直角三角形两锐角的关系.

练习册系列答案
相关题目
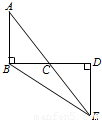
 (1)如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
(1)如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED. 如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.