题目内容
 (1)如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
(1)如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.(2)植树节期间,两所学校共植树834棵,其中海石中学植树的数量比励东中学的2倍少3棵,两校各植树多少棵?
分析:(1)根据已知条件可判断出△ABC≌△EDC,根据全等三角形的性质即可得出AB=ED,
(2)设励东中学植树x棵,可知海石中学植树2x-3颗,根据题意列出方程,解出x的值,即可得出结果.
(2)设励东中学植树x棵,可知海石中学植树2x-3颗,根据题意列出方程,解出x的值,即可得出结果.
解答:(1)证明:∵AB⊥BD,ED⊥BD
∴∠ABC=∠D=90°,
在△ABC和△EDC中
,
∴△ABC≌△EDC,
∴AB=ED;
(2)解:设励东中学植树x棵,
依题意,得x+(2x-3)=834,
解得x=279,
∴2x-3=2×279-3=555,
答:励东中学植树279棵,海石中学植树555棵.
∴∠ABC=∠D=90°,
在△ABC和△EDC中
|
∴△ABC≌△EDC,
∴AB=ED;
(2)解:设励东中学植树x棵,
依题意,得x+(2x-3)=834,
解得x=279,
∴2x-3=2×279-3=555,
答:励东中学植树279棵,海石中学植树555棵.
点评:本题考查了全等三角形的判定方法以及全等三角形的对应边相等,以及列方程解应用题,难度适中.

练习册系列答案
相关题目
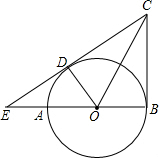 如图,AB是⊙O的直径,CB、CE分别切⊙O于点B、D,CE与BA的延长线交于点E,连接OC、OD.
如图,AB是⊙O的直径,CB、CE分别切⊙O于点B、D,CE与BA的延长线交于点E,连接OC、OD.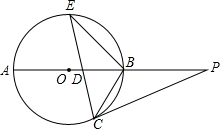 PA上截取PD=PC,连接CD,并延长交⊙O于点E.
PA上截取PD=PC,连接CD,并延长交⊙O于点E.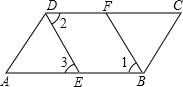
 19、如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论是( )
19、如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论是( ) 如图,AB、CD相交于点O,试添加一个条件使得△AOD∽△COB,你添加的条件是
如图,AB、CD相交于点O,试添加一个条件使得△AOD∽△COB,你添加的条件是