题目内容
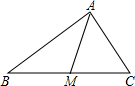 已知:如图所示,在△ABC中,M是BC边上的中点.
已知:如图所示,在△ABC中,M是BC边上的中点.求证:AM<
| 1 | 2 |
分析:延长AM到D,使MD=AM,连CD,根据SAS证△ABM≌△DCM,推出AB=CD,在△ACD中,根据三角形的三边关系定理得出AD<AC+CD,代入求出即可.
解答: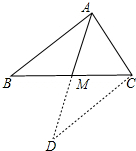 证明:延长AM到D,使MD=AM,连CD,
证明:延长AM到D,使MD=AM,连CD,
∵AM是BC边上的中线,
∴BM=CM,
∵在△ABM和△DCM中
∵
,
∴△ABM≌△DCM(SAS)
∴AB=CD,
在△ACD中,则AD<AC+CD,
即2AM<AC+AB,
∴AM<
(AB+AC).
 证明:延长AM到D,使MD=AM,连CD,
证明:延长AM到D,使MD=AM,连CD,∵AM是BC边上的中线,
∴BM=CM,
∵在△ABM和△DCM中
∵
|
∴△ABM≌△DCM(SAS)
∴AB=CD,
在△ACD中,则AD<AC+CD,
即2AM<AC+AB,
∴AM<
| 1 |
| 2 |
点评:本题考查了全等三角形的性质和判定,三角形的三边关系定理,解此题的关键是通过作辅助线把要求的线段放在一个三角形中,题目比较好.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 阅读下述说明过程,讨论完成下列问题:
阅读下述说明过程,讨论完成下列问题: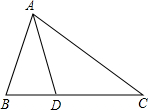 已知:如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
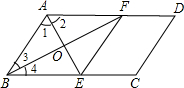
已知:如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.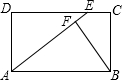 已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB.
已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB.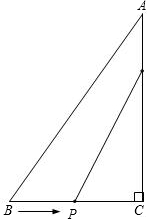 同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.
同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.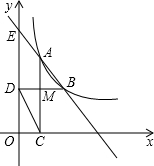 点M,连接DC.
点M,连接DC.