题目内容
已知:如图所示,在△ABC中,∠C=90°,BC=5cm,AC=7cm.两个动点P、Q分别从B、C两点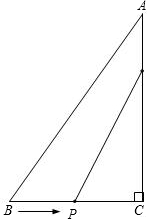 同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.
同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.(1)P、Q两点在运动过程中,经过几秒后,△PCQ的面积等于4厘米2?经过几秒后PQ的长度等于5厘米?
(2)在P、Q两点在运动过程中,四边形ABPQ的面积能否等于11厘米2?试说明理由.
(3)经过几秒时以C、P、Q为顶点的三角形与△ABC相似?
分析:(1)若使其面积为4,即S△PCQ=
PC•QC=4,代入数据求解即可;
(2)若四边形ABPQ的面积能否等于11,即S△PCQ=
-11=
,建立方程,解方程看是否有解,若有,则存在;
(3)要使三角形相似,其对应边成比例即可.
| 1 |
| 2 |
(2)若四边形ABPQ的面积能否等于11,即S△PCQ=
| 5×7 |
| 2 |
| 13 |
| 2 |
(3)要使三角形相似,其对应边成比例即可.
解答:解:(1)可设经x秒后其面积为4,
即
×(5-x)×2x=4,
解得x=1,
即经过1秒后,其面积等于4厘米2.
当经过t秒后PQ=5,
∵PC2+CQ2=PQ2,
∵PC=5-t,CQ=2t,PQ=5,
∴(5-t)2+(2t)2=52,
解得:t=0或2,
∴当经过0秒或2秒后PQ=5;
(2)若四边形ABPQ的面积能否等于11厘米2,即S△PCQ=
-11=
,
即
×(5-x)×2x=
,
化简得2x2-10x+13=0
△=b2-4ac=10×10-4×2×13<0,
所以此方程无解.
故四边形ABPQ的面积不能等于11厘米2.
(3)若两个三角形相似,当PQ∥AB,即
=
,
解得x=
.
当PQ不平行AB时,
=
解得:x=
即经过
或
秒后两三角形相似.
即
| 1 |
| 2 |
解得x=1,
即经过1秒后,其面积等于4厘米2.
当经过t秒后PQ=5,
∵PC2+CQ2=PQ2,
∵PC=5-t,CQ=2t,PQ=5,
∴(5-t)2+(2t)2=52,
解得:t=0或2,
∴当经过0秒或2秒后PQ=5;
(2)若四边形ABPQ的面积能否等于11厘米2,即S△PCQ=
| 5×7 |
| 2 |
| 13 |
| 2 |
即
| 1 |
| 2 |
| 13 |
| 2 |
化简得2x2-10x+13=0
△=b2-4ac=10×10-4×2×13<0,
所以此方程无解.
故四边形ABPQ的面积不能等于11厘米2.
(3)若两个三角形相似,当PQ∥AB,即
| 5-x |
| x |
| 2x |
| 7-2x |
解得x=
| 35 |
| 17 |
当PQ不平行AB时,
| 2x |
| 5-x |
| 5 |
| 7 |
解得:x=
| 25 |
| 19 |
即经过
| 35 |
| 17 |
| 25 |
| 19 |
点评:本题主要考查了相似三角形的判定及性质以及三角形的面积问题,能够熟练运用其性质求解一些简单的计算问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 阅读下述说明过程,讨论完成下列问题:
阅读下述说明过程,讨论完成下列问题: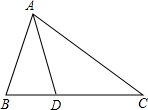 已知:如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
已知:如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.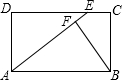 已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB.
已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB. 点M,连接DC.
点M,连接DC.