题目内容
 阅读下述说明过程,讨论完成下列问题:
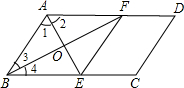
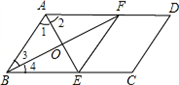
阅读下述说明过程,讨论完成下列问题:已知:如图所示,在?ABCD中,∠A的平分线与BC相交于点E,∠B的平分线与AD相交于点F,AE与BF相交于点O,试说明四边形ABEF是菱形.
证明:(1)∵四边形ABCD是平行四边形,
(2)∴AD∥BC.
(3)∴∠ABE+∠BAF=180°.
(4)∵AE、BF分别平分∠BAF、∠ABE,
(5)∴∠1=∠2=
| 1 |
| 2 |
| 1 |
| 2 |
(6)∴∠1+∠3=
| 1 |
| 2 |
| 1 |
| 2 |
(7)∴∠AOB=90°.
(8)∴AE⊥BF.
(9)∴四边形ABEF是菱形.
…
问:①上述说明过程是否正确?
答:
②如果错误,指出在第
分析:证得AE⊥BF,再证明AE与BF互相平分,根据“对角线平分且垂直的四边形是菱形”进行证明.
解答: 解:(1)不正确.
解:(1)不正确.
(2)⑧、⑨、⑧
∵在□ABCD中,AD∥BC,
∴∠AEB=∠2
又∵∠1=∠2,
∴∠1=∠AEB,
∴AB=BE
 解:(1)不正确.
解:(1)不正确.(2)⑧、⑨、⑧
∵在□ABCD中,AD∥BC,
∴∠AEB=∠2
又∵∠1=∠2,
∴∠1=∠AEB,
∴AB=BE
点评:菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:
①定义;
②四边相等;
③对角线互相垂直平分.
①定义;
②四边相等;
③对角线互相垂直平分.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
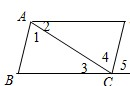 4、请阅读以下说明过程,并补全所空内容:
4、请阅读以下说明过程,并补全所空内容: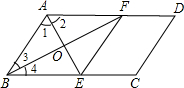 阅读下述说明过程,讨论完成下列问题:
阅读下述说明过程,讨论完成下列问题: ∠BAF,∠3=∠4=
∠BAF,∠3=∠4=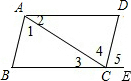
 ∠BAF,∠3=∠4=
∠BAF,∠3=∠4= ∠ABE.
∠ABE. (∠BAF+∠ABE)=
(∠BAF+∠ABE)= ×180°=90°.
×180°=90°.