题目内容
【题目】已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.

(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
【答案】解:(1)证明:连接AC,
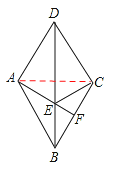
∵BD,AC是菱形ABCD的对角线,∴BD垂直平分AC。
∴AE=EC。
(2)点F是线段BC的中点。理由如下:
在菱形ABCD中,AB=BC,
又∵∠ABC=60°,∴△ABC是等边三角形。
∴∠BAC=60°。
∵AE=EC,∠CEF=60°,∴∠EAC=![]() ∠BAC=30°。
∠BAC=30°。
∴AF是△ABC的角平分线。
∵AF交BC于F,∴AF是△ABC的BC边上的中线。
∴点F是线段BC的中点。
【解析】
试题分析:(1)连接AC,根据菱形的对角线互相垂直平分可得BD垂直平分AC,再根据线段垂直平分线上的点到线段两端点的距离相等即可得证。
(2)先判定出△ABC是等边三角形,根据等边三角形的每一个角都是60°可得∠BAC=60°,再根据等边对等角以及三角形的一个外角等于与它不相邻的两个内角的和求出∠EAC=30°,从而判断出AF是△ABC的角平分线,再根据等边三角形的性质可得AF是△ABC的BC边上的中线,从而解得。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目



