Question

【题目】如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1 ， 边B1C1与CD交于点O，则四边形AB1OD的面积是（ ）

A.
B.
C.
D. ﹣1

Answer 1

【答案】D
【解析】方法一：
解：连接AC1 ，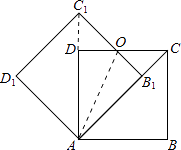

∵四边形AB1C1D1是正方形，
∴∠C1AB1= ×90°=45°=∠AC1B1 ，
∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1 ，
∴∠B1AB=45°，
∴∠DAB1=90°﹣45°=45°，
∴AC1过D点，即A、D、C1三点共线，
∵正方形ABCD的边长是1，
∴四边形AB1C1D1的边长是1，
在Rt△C1D1A中，由勾股定理得：AC1= = ，
则DC1= ﹣1，
∵∠AC1B1=45°，∠C1DO=90°，
∴∠C1OD=45°=∠DC1O，
∴DC1=OD= ﹣1，
∴S△ADO= ×ODAD= ，
∴四边形AB1OD的面积是=2× = ﹣1，
方法二：
解：∵四边形ABCD是正方形，
∴AC= ，∠OCB1=45°，
∴CB1=OB1
∵AB1=1，
∴CB1=OB1=AC﹣AB1= ﹣1，
∴S△OB1C= OB1CB1= （ ﹣1）2 ，
∵S△ADC= ADAC= ×1×1= ，
∴S四边形AB1OD=S△ADC﹣S△OB1C= ﹣ （ ﹣1）2= ﹣1；
故选：D．
连接AC1 ， AO，根据四边形AB1C1D1是正方形，得出∠C1AB1=∠AC1B1=45°，求出∠DAB1=45°，推出A、D、C1三点共线，在Rt△C1D1A中，由勾股定理求出AC1 ， 进而求出DC1=OD，根据三角形的面积计算即可．