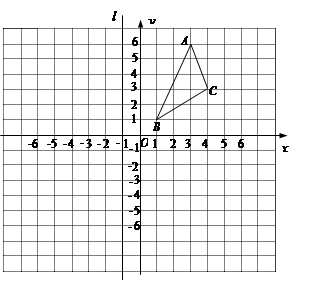题目内容
如图,E点是正方形ABCD的边BC上一点,AB=12,BE=5,△ABE逆时针旋转后能够与△ADF重合.

(1)旋转中心是 ,旋转角为 度;
(2)△AEF是 三角形;
(3)求EF的长.

(1)旋转中心是 ,旋转角为 度;
(2)△AEF是 三角形;
(3)求EF的长.
详见解析
试题分析:(1)如图△ABE逆时针旋转后能够与△ADF重合,可知旋转中心是点A;边AB与边AD重合,可知旋转角为900.(2)由旋转可知:AE=AF,∠BAE=∠DAF,所以∠EAF=900.所以ΔAEF是等腰直角三角形.
(3)根据(1)(2)可知只要知道AE的长度,利用勾股定理即可求解.而AE是RtΔABE的斜边,AB=12,BE=5,因此可求AE.这样求EF的长度就迎刃而解了.
试题解析:
解:(1)点A,90°
等腰直角
(3)由旋转可知∠EAF=90°,△ABE≌△ADF,
∴AE=AF,△EAF是等腰直角三角形
在Rt△ABE中,∵AB=12,BE=5
∴
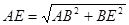
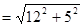

∴
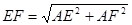
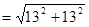
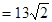

练习册系列答案
相关题目