题目内容
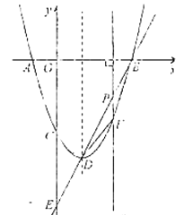
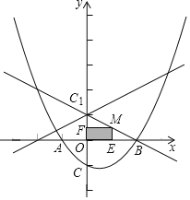
【题目】如图,已知抛物线y=ax2+bx﹣1与x轴的交点为A(﹣1,0),B(2,0),且与y轴交于C点.
(1)求该抛物线的表达式;
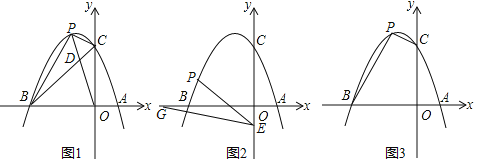
(2)点C关于x轴的对称点为C1,M是线段BC1上的一个动点(不与B、C1重合),ME⊥x轴,MF⊥y轴,垂足分别为E、F,当点M在什么位置时,矩形MFOE的面积最大?说明理由.
(3)已知点P是直线y=![]() x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.
x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.
【答案】(1) ![]() ;(2)点M为线段C1B中点时,S矩形MFOE最大,理由见解析;(3) 点P和点Q的坐标为P1(4,3),Q1(4,5)或P2(﹣2,0),Q2(﹣2,2)或P3(2,2),Q3(2,0)或P4(﹣2,0),Q4(2,0).
;(2)点M为线段C1B中点时,S矩形MFOE最大,理由见解析;(3) 点P和点Q的坐标为P1(4,3),Q1(4,5)或P2(﹣2,0),Q2(﹣2,2)或P3(2,2),Q3(2,0)或P4(﹣2,0),Q4(2,0).
【解析】
(1)将A(﹣1,0),B(2,0)分别代入解析式即可解答
(2)令x=0,y=﹣1,得出C的坐标,再利用对称轴的性质得出C1,将B(2,0),C1(0,1)分别代入直线C1B解析式,得出直线C1B的解析式,设M(t,![]() ),则 E(t,0),F(0,
),则 E(t,0),F(0,![]() ),根据矩形的面积公式即可解答
),根据矩形的面积公式即可解答
(3)根据题意可分情况讨论①当C1C为边,则C1C∥PQ,C1C=PQ,设P(m,![]() m+1),Q(m,
m+1),Q(m,![]() ),求出m即可解答;②C1C为对角线,∵C1C与PQ互相平分,C1C的中点为(0,0),PQ的中点为(0,0),设P(m,
),求出m即可解答;②C1C为对角线,∵C1C与PQ互相平分,C1C的中点为(0,0),PQ的中点为(0,0),设P(m,![]() m+1),则Q(﹣m,
m+1),则Q(﹣m,![]() ),求出m即可
),求出m即可
(1)将A(﹣1,0),B(2,0)分别代入抛物线y=ax2+bx﹣1中,得![]() ,解得:
,解得:
∴该抛物线的表达式为:![]() .
.
(2)在![]() 中,令x=0,y=﹣1,∴C(0,﹣1)
中,令x=0,y=﹣1,∴C(0,﹣1)
∵点C关于x轴的对称点为C1,
∴C1(0,1),设直线C1B解析式为y=kx+b,将B(2,0),C1(0,1)分别代入得![]() ,解得
,解得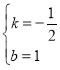 ,
,
∴直线C1B解析式为![]() ,设M(t,
,设M(t,![]() ),则 E(t,0),F(0,
),则 E(t,0),F(0,![]() )
)
∴S矩形MFOE=OE×OF=t(![]() )=﹣
)=﹣![]() (t﹣1)2+
(t﹣1)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当t=1时,S矩形MFOE最大值=![]() ,此时,M(1,
,此时,M(1,![]() );即点M为线段C1B中点时,S矩形MFOE最大.
);即点M为线段C1B中点时,S矩形MFOE最大.
(3)由题意,C(0,﹣1),C1(0,1),以C、C1、P、Q为顶点的四边形为平行四边形,分以下两种情况:
①C1C为边,则C1C∥PQ,C1C=PQ,设P(m,![]() m+1),Q(m,
m+1),Q(m,![]() ),
),
∴|(![]() )﹣(
)﹣(![]() m+1)|=2,解得:m1=4,m2=﹣2,m3=2,m4=0(舍),
m+1)|=2,解得:m1=4,m2=﹣2,m3=2,m4=0(舍),
P1(4,3),Q1(4,5);P2(﹣2,0),Q2(﹣2,2);P3(2,2),Q3(2,0)
②C1C为对角线,∵C1C与PQ互相平分,C1C的中点为(0,0),
∴PQ的中点为(0,0),设P(m,![]() m+1),则Q(﹣m,
m+1),则Q(﹣m,![]() )
)
∴(![]() m+1)+(
m+1)+(![]() )=0,解得:m1=0(舍去),m2=﹣2,
)=0,解得:m1=0(舍去),m2=﹣2,
∴P4(﹣2,0),Q4(2,0);
综上所述,点P和点Q的坐标为:P1(4,3),Q1(4,5)或P2(﹣2,0),Q2(﹣2,2)或P3(2,2),Q3(2,0)或P4(﹣2,0),Q4(2,0).

 阅读快车系列答案
阅读快车系列答案