题目内容
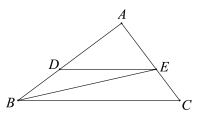
【题目】在
中，
，AE垂直于AB边上的中线CD，交BC于点E.
（1）求证：
（2）若
，求边AC与BC的长.
【答案】（1）详见解析；（2）
【解析】
(1)先说明△ACB∽△ECA，然后运用相似三角形的性质即可解答；
(2) 在Rt△ABC的中线，运用勾股定理求出AB，再说明△DFC∽△ECA，运用相似三角形的性质即可解答。
解：（1）因为CD是AB边上的中线，
所以CD＝DB，
∠ABC＝∠DCB＝∠CAE，
∠ACB＝∠ECA＝
，
所以△ACB∽△ECA，
所以
，
所以
（2）因为CD是Rt△ABC的中线，
所以CD=AD=BD.
所以AB=6.
所以
取BC中点F，连结DF，则DF//AC，∠DFC＝∠ECA＝，
所以△DFC∽△ECA，
所以
．
所以
故可解得
，
．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
【题目】体育组为了了解九年级450名学生排球垫球的情况，随机抽查了九年级部分学生进行排球垫球测试（单位：个），根据测试结果，制成了下面不完整的统计图表：
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
（1）表中的数
，
；
（2）估算该九年级排球垫球测试结果小于10的人数；
（3）排球垫球测试结果小于10的为不达标，若不达标的5人中有3个男生，2个女生，现从这5人中随机选出2人调查，试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率．
