题目内容
【题目】已知Rt△ABC≌Rt△DBE,∠ACB=∠DEB=90°,∠A=∠D.
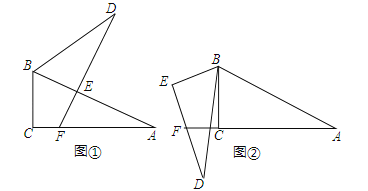
(1)将两三角形按图①方式摆放,其中点E落在AB上,DE所在直线交边AC于点F.求证:AF+EF=DE;
(2)若将两三角形按照图②方式摆放,边AC的延长线与DE相交于点F.你认为(1)中的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
【答案】(1)证明见试题解析;(2)不成立.此时AF、EF与DE的关系为AF=EF+DE.
【解析】
试题分析:(1)由Rt△ABC≌Rt△DBE推出BC=BE,连接BF,由HL证Rt△BCF≌Rt△BEF,推出CF=EF即可;
(2)猜想(1)结论不成立,关系式是AF=EF+DE,连接BF,由HL证Rt△BEF≌Rt△BCF,推出EF=FC,由AF=AC+FC可推出AF=DE+EF.
试题解析:(1)证明:连接BF.由Rt△ABC≌Rt△DBE知:BC=BE.在Rt△BCF和Rt△BEF中,∵BC=BE,BF=BF,∴Rt△BCF≌Rt△BEF(HL),∴CF=EF,∵AC=DE,CF+FA=CA,∴AF+EF=DE;
(2)解:(1)中猜想结论不成立,关系式是AF=EF+DE.理由是:
连接BF.在Rt△BEF和Rt△BCF中,∵BC=BE,BF=BF,∴Rt△BEF≌Rt△BCF(HL),∴EF=FC,∵AC=DE,由AF=AC+FC知:AF=DE+EF.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目