Question

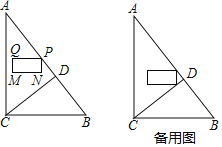
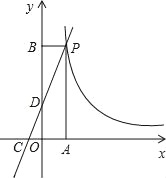
【题目】如图，在三角形ABC中，∠A=90°，AB=AC=2，将△ABC折叠，使点B落在边AC上点D （不与点A重合）处，折痕为PQ，当重叠部分△PQD为等腰三角形时，则AD的长为_____．

Answer 1

【答案】2或2﹣2．

【解析】

分①PD=DQ；②DQ=PQ；③PD=PQ三种情况结合已知条件分析解答即可.

若△PDQ为等腰三角形，则存在以下三种情况：

（1）当PD=DQ时，

由折叠的性质可知，PD=PB，DQ=BQ，

∴PD=PB=BQ=DQ，

∴四边形BQDP是菱形，

∴PD∥BC，BP∥DQ，
∵∠A=90°，AB=AC，
∴△ABC是等腰直角三角形，
∴△APD和△CDQ都是等腰直角三角形，

设AD=x，则AP=x，PD=PB=2-x，

在Rt△APD中，由勾股定理可得：，

解得：（不合题意，舍去），

∴此时AD=；

（2）DQ=PQ时，

由折叠的性质可知：BQ=DQ=PQ，

又∵在△ABC中，∠B=45°，
∴∠BPQ=∠B=45°，
∴∠PQB=90°，

∴PQ⊥BC，

∵将点B沿PQ折叠后点B落在AC上，

∴点B与点C重合，

∴x=AD=AC=2；

（3）当PD=PQ时，