题目内容
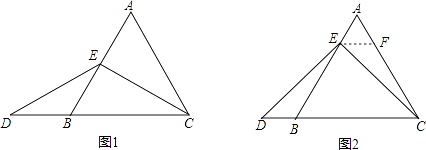
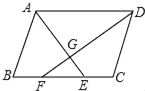
【题目】如图,在ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.
(1)求证:∠AGD=90°.
(2)若CD=4cm,求BE的长.
【答案】(1)见解析;(2)BE=4cm,
【解析】
(1)由平行四边形的性质和角平分线即可得出结论;
(2)利用平行四边形的性质结合角平分线的性质得出∠BAE=∠BEA,∠CFD=∠CDF,进而求出AB=BE=CD=4cm即可.
(1)证明:∵四边形ABCCD是平行四边形,
∴∠BAD+∠ADC=180°,
∵AE、DF分别是∠BAD、∠ADC的平分线,
∴∠DAG=![]() ∠BAD,∠ADG=
∠BAD,∠ADG=![]() ∠ADC,
∠ADC,
∴∠DAG+∠ADG=![]() ×(∠BAD+∠ADC)=
×(∠BAD+∠ADC)=![]() ×180°=90°,
×180°=90°,
∴∠AGD=90°;
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∵CD=4cm,
∴BE=4cm,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目