题目内容
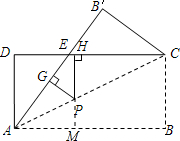
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
(1)试找出一个与△AED全等的三角形,并加以证明;
(2)若AB=8,DE=3,P为线段AC上的一个动点,过点P作PG⊥AB′于点G,作PH⊥DC于点H,试判断PG+PH的值是否为定值?若为定值,请求出这个定值;若不是定值,请说明理由.

(1)试找出一个与△AED全等的三角形,并加以证明;
(2)若AB=8,DE=3,P为线段AC上的一个动点,过点P作PG⊥AB′于点G,作PH⊥DC于点H,试判断PG+PH的值是否为定值?若为定值,请求出这个定值;若不是定值,请说明理由.

(1)△CEB′≌△AED.
证明:由折叠和四边形ABCD为矩形可得:
AD=B′C,∠D=∠B′=90°,
在△CEB′和△AED中,
,
∴△CEB′≌△AED(AAS).
(2)PG+PH的值是定值.
①当点P不与点A、C重合时,
延长HP交AB于点M,则PM⊥AB.
∵∠EAC=∠CAB,PG⊥AB′于点G,
∴PG=PM.
∴PG+PH=PM+PH=HM=AD.
∵∠EAC=∠CAB,∠CAB=∠ECA,
∴∠EAC=∠ECA.
∴AE=EC=DC-DE=AB-DE=8-3=5.
在Rt△ADE中,AD=
=
=4.
∴PG+PH=AD=4.
②当点P与点A重合时,点G与点A重合,点H与点D重合,
∴PG+PH=0+AD=4.
③当点P与点C重合时,点G与点B′重合,点H与点C重合,
∴PG+PH=B′C=BC=AD=4.
综上说述,PG+PH的值是定值,且PG+PH=4.
证明:由折叠和四边形ABCD为矩形可得:
AD=B′C,∠D=∠B′=90°,
在△CEB′和△AED中,
|
∴△CEB′≌△AED(AAS).
(2)PG+PH的值是定值.
①当点P不与点A、C重合时,
延长HP交AB于点M,则PM⊥AB.
∵∠EAC=∠CAB,PG⊥AB′于点G,
∴PG=PM.
∴PG+PH=PM+PH=HM=AD.
∵∠EAC=∠CAB,∠CAB=∠ECA,
∴∠EAC=∠ECA.
∴AE=EC=DC-DE=AB-DE=8-3=5.
在Rt△ADE中,AD=
| AE2-DE2 |
| 52-32 |
∴PG+PH=AD=4.
②当点P与点A重合时,点G与点A重合,点H与点D重合,
∴PG+PH=0+AD=4.
③当点P与点C重合时,点G与点B′重合,点H与点C重合,
∴PG+PH=B′C=BC=AD=4.
综上说述,PG+PH的值是定值,且PG+PH=4.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





 其一面着色.
其一面着色.
