题目内容
【题目】已知点![]() 的坐标为
的坐标为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为
为![]() 的中点,双曲线
的中点,双曲线![]() 经过
经过![]() 、
、![]() 两点.
两点.

(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)如图1,点![]() 在
在![]() 轴上,若四边形
轴上,若四边形![]() 是平行四边形,求点
是平行四边形,求点![]() 的坐标;
的坐标;
(3)如图2,在(2)的条件下,动点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,若以
轴上,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,试求满足要求的所有点
为顶点的四边形为平行四边形,试求满足要求的所有点![]() 、
、![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 、
、![]() 坐标分别为
坐标分别为![]() 、
、![]() ;
;![]() 、
、![]() 或、
或、![]() 、
、![]()
【解析】
(1) 过点![]() 作
作![]() 轴于
轴于![]() ,再证
,再证![]() ,即可求出
,即可求出![]() 、
、![]() 、
、![]() 的值;
的值;
(2) 设![]() 得到
得到![]() ,即可求出点
,即可求出点![]() 的坐标;
的坐标;
(3)由反比例函数的解析式为![]() ,再由点P在双曲线
,再由点P在双曲线![]() 上,点Q在y轴上,设Q(0,y), P(x,
上,点Q在y轴上,设Q(0,y), P(x, ![]() ),再分以AB为边和以AB为对角线两种情况求出x的值,故可得出P、Q的坐标.
),再分以AB为边和以AB为对角线两种情况求出x的值,故可得出P、Q的坐标.
解:(1)过点![]() 作
作![]() 轴于
轴于![]()
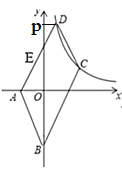
∵![]() 为
为![]() 的中点,
的中点,
∴DE=AE,
又∵∠PED=∠OEA, ∠DPE=∠AOE,
∴![]()
∴![]()
∴![]()
![]()
∴![]() 即
即![]()
∴![]()
(2)∵四边形![]() 是平行四边形.
是平行四边形.
∴![]()
∵![]()
![]()
![]()
![]() 在
在![]() 轴上
轴上
∴设![]()
则![]()
![]()
∴![]()
(3)∵反比例函数的表达式为![]() ,
,
∵点P在双曲线![]() 上,点Q在y轴上,
上,点Q在y轴上,
∴设![]() );
);
①AB为边时,如图①所示.若四边形ABPQ平行四边形,
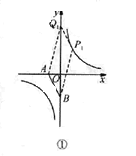
则![]() =0,解得x=1,此时P1(1,4),Q1(0,6);
=0,解得x=1,此时P1(1,4),Q1(0,6);
如图②所示.
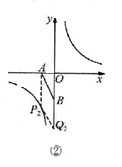
若四边形ABQP是平行四边形,则x=1.此时P2(1,4),Q2(0,6);
②当AB为对角线时,如图③所示,
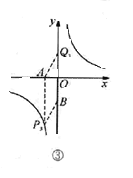
AP=BQ,且AP//BQ,
所以x=1,
所以P3(1,4),Q3(0,2),
故满足要求的点P,Q的坐标分别是![]() 、
、![]() ;
;![]() 、
、![]() 或、
或、![]() 、
、![]()
.

练习册系列答案
相关题目










