题目内容
如图,已知C是线段AB上一点,点D和点E分别是AC、CB的中点,若AC=4cm,CB=3cm,求线段DE的长.
解:∵点D是AC的中点,AC=4cm,
∴DC= AC=2cm;
AC=2cm;
又点E是CB的中点,CB=3cm,
∴CE= CB=1.5cm;
CB=1.5cm;
∵DE=DC+CE,
∴DE=3.5cm.
分析:根据图示找出DE与AC、CB的数量关系,然后将已知数值代入解答即可.
点评:本题主要考查了两点间的距离的计算,在解答此题时,采用了数形结合的数学思想.
∴DC=
 AC=2cm;
AC=2cm;又点E是CB的中点,CB=3cm,
∴CE=
 CB=1.5cm;
CB=1.5cm;∵DE=DC+CE,
∴DE=3.5cm.
分析:根据图示找出DE与AC、CB的数量关系,然后将已知数值代入解答即可.
点评:本题主要考查了两点间的距离的计算,在解答此题时,采用了数形结合的数学思想.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
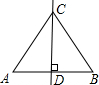 如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )
如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )| A、AE=BE | B、AD=BD | C、AB=AC | D、ED=AD |
如图,已知C是线段AB的中点,则CD等于( )


| A、AD-BD | ||
B、
| ||
C、
| ||
D、AD-
|
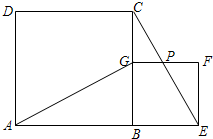 如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE.
如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE. (2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1
(2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1