Question

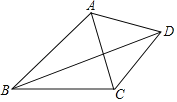
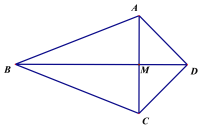
【题目】如图，四边形ABCD中， BA=BC， DA=DC，我们把这种两组邻边分别相等的四边形叫做“筝形”， 其对角线AC、BD交于点M，请你猜想关于筝形的对角线的一条性质，并加以证明.

猜想：

证明：

Answer 1

【答案】筝形有一条对角线平分一组对角，即BD平分∠ABC且BD平分∠ADC；证明见解析

【解析】

利用SSS定理证明△ABD≌△CBD，可得∠ABD=∠CBD，∠ADB=∠CDB，从而可写出关于筝形的对角线的一条性质，筝形有一条对角线平分一组对角.

解：筝形有一条对角线平分一组对角，即BD平分∠ABC且BD平分∠ADC

证明：∵在△ABD和△CBD中

BA=BC，DA=DC，BD=BD

∴△ABD≌△CBD(SSS)

∴∠ABD=∠CBD，∠ADB=∠CDB

即BD平分∠ABC，且BD平分∠ADC.