题目内容
【题目】如图1,四边形ABCD为菱形,E为对角线AC上的一个动点,连接DE并延长交射线AB于点F,连接BE. 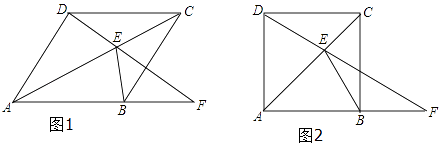
(1)求证:∠F=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠F的度数(如图2).
【答案】
(1)证明:∵四边形ABCD是菱形,
∴CD=AB,∠ACD=∠ACB,
在△DCE和△BCE中,
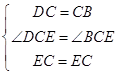 ,
,
∴△DCE≌△BCE(SAS),
∴∠CDE=∠CBE,
∵CD∥AB,
∴∠CDE=∠AFD,
∴∠EBC=∠AFD,即∠F=∠EBC;
(2)解:分两种情况:
①如图1,当F在AB延长线上时,
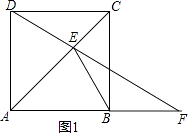
∵∠EBF为钝角,
∴只能是BE=BF,
设∠BEF=∠BFE=x°,
可通过三角形内角形为180°得:90+x+x+x=180,
解得:x=30,
∴∠EFB=30°;
②如图2,当F在线段AB上时,

∵∠EFB为钝角,
∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°,
可证得:∠AFD=∠FDC=∠CBE,
得x+2x=90,
解得:x=30,
∴∠EFB=120°.
综上:∠F=30°或120°.
【解析】(1)直接利用全等三角形的判定方法得出△DCE≌△BCE(SAS),即可得出答案;(2)利用正方形的性质结合等腰三角形的性质得出:①当F在AB延长线上时;②当F在线段AB上时;分别求出即可.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目
【题目】某果农种了50棵苹果树,收获时,他把苹果树的产量做了一下统计,得到下表:
质量(千克) | 33 | 34 | 35 | 36 | 38 |
数量(棵) | 10 | 5 | 20 | 10 | 5 |
(1)苹果产量的众数是;中位数是;平均数是;
(2)市场上苹果的销售价为8元/千克,化肥、农药、人工费等共投入资金1000元,则今年该果农纯收入多少元?