Question

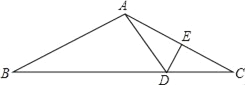
【题目】已知点E为正方形ABCD的边AD上一点，连接BE，过点C作CN⊥BE，垂足为M，交AB于点N．

（1）求证：△ABE≌△BCN；

（2）若N为AB的中点，求tan∠ABE．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）根据正方形的性质得到AB＝BC，∠A＝∠CBN＝90°，∠1＋∠2＝90°，根据垂线和三角形内角和定理得到∠2＋∠3＝90°，推出∠1＝∠3，根据ASA推出△ABE≌△BCN；（2）tan∠ABE＝，根据已知求出AE与AB的关系即可求得tan∠ABE.

（1）证明：∵四边形ABCD为正方形

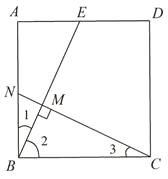
∴AB=BC，∠A=∠CBN=90°，∠1+∠2=90°

∵CM⊥BE，

∴∠2+∠3=90°

∴∠1=∠3

在△ABE和△BCN中，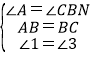

∴△ABE≌△BCN（ASA）；

（2）∵N为AB中点，

∴BN=AB

又∵△ABE≌△BCN，

∴AE=BN=AB

在Rt△ABE中，tan∠ABE═．