题目内容
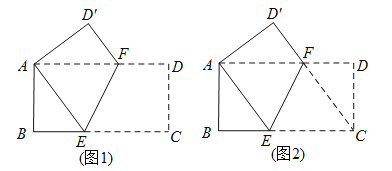
【题目】已知,如图,等腰Rt△ABC,等腰Rt△ADE,AB⊥AC,AD⊥AE,AB=AC,AD=AE,CD交AE、BE分别于点M、F
(1)求证:△DAC≌△EAB;
(2)若∠AEF=15°,EF=4,求DE的长.

【答案】(1)见解析;(2)DE=8.
【解析】
(1)根据SAS证明△DAC≌△EAB即可;
(2)利用“8字型”证明∠EFM=∠DAM=90°,再证明DE=2EF即可解决问题;
(1)证明:∵∠DAE=∠BAC=90°,
∴∠DAC=∠EAB,
在△DAC和△EAB中,
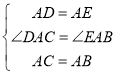 ,
,
∴△DAC≌△EAB(SAS).
(2)∵△DAC≌△EAB(已证),
∴∠ADC=∠AEB,
∵∠AMD=∠EMF,
∴∠DAM=∠EFM=90°,
∵∠AED=45°,∠AEF=15°,
∴∠DEF=60°,∠FDE=30°,
∴DE=2FE=8.

练习册系列答案
相关题目
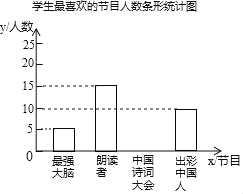
【题目】为了解某校中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:根据以上提供的信息,解答下列问题:
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
(1)x= ,a= ,b= ;
(2)补全上面的条形统计图;
(3)在喜爱《最强大脑》的学生中,有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加潍坊市组织的竞赛活动,请用树状图或列表法求出所抽取的2名同学恰好是1名男同学和1名女同学的概率.