��Ŀ����
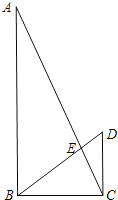
����Ŀ������ABC�У�AB=AC����D�ڱ�BC���ڵ�ֱ���ϣ�����D��DF��AC��ֱ��AB�ڵ�F��DE��AB��ֱ��AC�ڵ�E��
��1������D�ڱ�BC��ʱ����ͼ�٣���֤��DE+DF=AC��
��2������D�ڱ�BC���ӳ�����ʱ����ͼ�ڣ�����D�ڱ�BC�ķ����ӳ�����ʱ����ͼ�ۣ���ֱ�д��ͼ�ڡ�ͼ����DE��DF��AC֮���������ϵ������Ҫ֤����
��3����AC=6��DE=4����DF= ��
���㣺ƽ���ı��ε��ж������ʣ�ȫ�������ε��ж������ʣ����������ε����ʣ�
���𰸡���1��֤����������2��ͼ���У�AC+DE=DF��ͼ���У�AC+DF=DE��3��2��10
��������
�������:��1��֤���ı���AFDE��ƽ���ı��Σ�����DEC����BDF�ǵ��������μ���֤�ã�
��2���루1����֤��������ͬ��
��3�����ݣ�1����2���еĽ���ֱ����⣮
�⣺��1��֤������DF��AC��DE��AB��
���ı���AFDE��ƽ���ı��Σ�
��AF=DE��
��DF��AC��
���FDB=��C
����AB=AC��
���B=��C��
���FDB=��B
��DF=BF
��DE+DF=AB=AC��
��2��ͼ���У�AC+DE=DF��
ͼ���У�AC+DF=DE��
��3������ͼ�ٵ������DF=AC��DE=6��4=2��
����ͼ�ڵ������DF=AC+DE=6+4=10��
�ʴ��ǣ�2��10��

 ������ϵ�д�
������ϵ�д�