Question

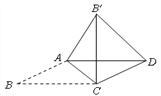
【题目】如图，平行四边形ABCD中，∠B＝30°，AB ≠ BC ，将△ABC沿AC翻折至△AB′C ，连结B ′D. 若，∠AB ′D＝75°，则BC =_____________．

Answer 1

【答案】．

【解析】试题分析：根据对折的性质求得∠AB′C=30°，从而求得∠CB′D=45°，由于B′D∥AC，得出∠ACB′=∠CB′D=45°，进而即可求得∠ACB=45°；作AG⊥BC于G，解直角三角形即可求得BC．

解：如图∵四边形ABCD是平行四边形，

∴AB=CD，BC=AD，∠B=∠ADC，

∵将△ABC沿AC翻折至△AB′C，

∴AB′=AB，B′C=BC，∠AB′C=∠B，

∴AB′=CD，B′C=AD，∠AB′C=∠ADC，

在△AB′C和△CAD中，

，

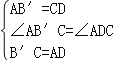∴△AB′C≌△CAD（SAS），

∴∠ACB′=∠CAD，

设AD、B′C相交于E，

∴AE=CE，

∴△ACE是等腰三角形，

即△AB′C与ABCD重叠部分的图形是等腰三角形；

∵B′C=AD，AE=CE，

∴B′E=DE，

∴∠CB′D=∠ADB′，

∵∠AEC=∠B′ED，∠ACB′=∠CAD，

∴∠ADB′=∠DAC，

∴B′D∥AC；

∵在ABCD中，∠B=30°，将△ABC沿AC翻折至△AB′C，

∴∠AB′C=30°，

∵∠AB′D=75°，

∴∠CB′D=45°，

∵B′D∥AC，

∴∠ACB′=∠CB′D=45°，

∵∠ACB=∠ACB′，

∴∠ACB=45°；

作AG⊥BC于G，

∴AG=CG，

∵∠B=30°，

∴AG=AB=，

∴CG=，BG=3，

∴BC=BG+CG=3+．

故答案为：．