题目内容
【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.
(1)求BE的长度;
(2)求△ABE的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由CD⊥BC,得到∠DCB为直角,在直角三角形BCD中,利用勾股定理求出BD的长,根据AB与CD平行,得到三角形ABE与三角形CDE相似,由相似得比例,求出BE的长即可;
(2)作EF垂直于AB,EH垂直于CD,由三角形ABE与三角形CDE相似,得比例,把BC的长代入求出EF的长,即可求出三角形ABE面积.
解:(1)∵CD⊥BC,
∴∠DCB=90°,
在Rt△BCD中,BC=4,DC=3,
根据勾股定理得:BD=![]() =5,
=5,
∵AB∥CD,
∴△ABE∽△CDE,
∴DC:AB=DE:BE=3:9=1:3,
又∵BD=5,
∴BE=![]() BD=
BD=![]() ;
;
(2)作EF⊥AB,EH⊥CD,
∵△ABE∽△CDE,
∴EF:EH=DC:AB=1:3,
又∵BC=4,
∴FE=![]() BC=3,
BC=3,
则S△ABE=AB×EF×![]() =
=![]() .
.
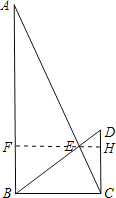

练习册系列答案
相关题目