Question

【题目】如图，正方形ABCD中，AB=4，P是CD边上的动点（P点不与C、D重合），过点P作直线与BC的延长线交于点E，与AD交于点F，且CP=CE，连接DE、BP、BF，设CP═x，△PBF的面积为S1 ，△PDE的面积为S2 ．

（1）求证：BP⊥DE．

（2）求S1﹣S2关于x的函数解析式，并写出x的取值范围．

（3）分别求当∠PBF=30°和∠PBF=45°时，S1﹣S2的值．

Answer 1

【答案】（1）证明见解析；（2）S1﹣S2= x2（0＜x＜4）；（3）①当∠PBF=30°时，S1﹣S2=；②当∠PBF=45°时，S1﹣S2=．

【解析】试题分析：（1）首先延长BP交DE于M．然后依据SAS可证明△BCP≌△DCE，依据全等三角形的性质可得到∠BCP=∠CDE，由∠CBP+∠CPB=90°，∠CPB=∠DPM，即可推出∠CDE+∠DPM=90°；

（2）根据题意可得到S1-S2=S△PBE-S△PDE，然后依据三角形的面积公式列出函数关系式即可；

（3）分当∠PBF=30°和∠PBF=45°两种情形分别求出PC的长，最后再利用（2）中结论进行计算即可.

试题解析：（1）如图1中，延长BP交DE于M，

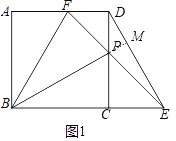
∵四边形ABCD是正方形，

∴CB=CD，∠BCP=∠DCE=90°，

∵CP=CE，

∴△BCP≌△DCE，

∴∠BCP=∠CDE，

∵∠CBP+∠CPB=90°，∠CPB=∠DPM，

∴∠CDE+∠DPM=90°，

∴∠DMP=90°，

∴BP⊥DE；

（2）由题意S1﹣S2=（4+x）x﹣ （4﹣x）x=x2（0＜x＜4）；

（3）①如图2中，当∠PBF=30°时，

∵∠CPE=∠CEP=∠DPF=45°，∠FDP=90°，

∴∠PFD=∠DPF=45°，

∴DF=DP，∵AD=CD，

∴AF=PC，∵AB=BC，∠A=∠BCP=90°，

∴△BAF≌△BCP，

∴∠ABF=∠CBP=30°，

∴x=PC=BCtan30°=，

∴S1﹣S2=x2=；

②如图3中，当∠PBF=45°时，在CB上截取CN=CP，连接PN，

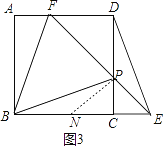
由①可知△ABF≌△BCP，

∴∠ABF=∠CBP，

∵∠PBF=45°，

∴∠CBP=22.5°，

∵∠CNP=∠NBP+∠NPB=45°，

∴∠NBP=∠NPB=22.5°，

∴BN=PN=x，

∴x+x=4，

∴x=4 ﹣4，

∴S1﹣S2=（4 ﹣4）2=48﹣32 ．