题目内容
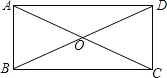
【题目】如图,矩形ABCD的对角线相交于点O,BD=6,AD=3![]() ,则∠AOD= 度.
,则∠AOD= 度.
【答案】120
【解析】
试题分析:由矩形的性质可推出∠ABC=90°,由特殊角的锐角三角函数值可求出∠ACB=30°,根据矩形性质求出OB=OC,求出∠OBC和∠OCB的度数,求出∠BOC,即可求出∠AOD.
证明:∵四边形ABCD是矩形,
∴∠ABC=90°(矩形的四个角都是直角),BD=AC,AD=BC,
∵在Rt△ABC中,BD=6,AD=3![]() ,
,
∴cos∠ACB=![]() =
=![]() ,
,
∴∠ACB=30°,
∵四边形ABCD是矩形,
∴OB=OD=![]() BD,OC=OA=AC,AC=BD,
BD,OC=OA=AC,AC=BD,
∴BO=CO,
∴∠OBC=∠OCB=30°,
∵∠OBC+∠OCB+∠BOC=180°,
∴∠BOC=120°,
∴∠AOD=∠BOC=120°,
故答案为:120.

练习册系列答案
相关题目