题目内容
【题目】如图,在平面直角坐标系xOy中,点O为坐标原点,直线y=-x+4与x轴交于点A,与y轴交于点B.
(1)求点A,B的坐标;
(2)在直线AB上是否存在点P,使△OAP是以OA为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若将Rt△AOB折叠,使OB边落在AB上,点O与点D重合,折痕为BC,求点C的坐标。
(4)直接写出折痕BC所在直线的表达式.

【答案】(1) A(4,0),B(0,4); (2) P点坐标为(2,2); (3) C(4![]() 4,0);(4) 折痕BC的解析式为y=-(1+
4,0);(4) 折痕BC的解析式为y=-(1+![]() )x+4.
)x+4.
【解析】
(1)利用直线解析式,容易求得A、B的坐标;
(2)作线段OA的垂直平分线,交x轴于点E,交AB于点P,则P点即为所求,可求得E点坐标,则容易求得P点坐标;
(3)可设C(t,0),由折叠的性质可得到CD=t,AC=4-t,在Rt△ACD中,由勾股定理可得到关于t的方程,可求得t的值,则可求得C点坐标;
(4)利用待定系数法可求得直线BC的解析式.
解:(1)在y=x+4中,令x=0可得y=4,令y=0可求得x=4,
∴A(4,0),B(0,4);
(2)如图1,作线段OA的垂直平分线,交x轴于点E,交AB于点P,
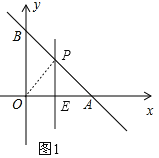
则OP=PA,即P点即为满足条件的点,
∵OA=4,
∴OE=2,
在y=x+4中,当x=2时,可得y=2,
∴P点坐标为(2,2);
(3)设C(t,0),则AC=OAOC=4t,
∵OA=OB=4,
∴AB=4![]() ,
,
由折叠的性质可得BD=OB=4,CD=OC=t,∠ADC=∠BOC=90,
∴AD=ABBD=4![]() 4,
4,
在Rt△ACD中,由勾股定理可得AC2=AD2+CD2,即(4t)2=t2+(4![]() 4)2,
4)2,
解得t=4![]() 4,
4,
∴C(4![]() 4,0),
4,0),
(4) 设直线BC解析式为y=kx+b,
∵B(0,4),C(4![]() 4,0)
4,0)
∴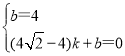
解得: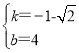
折痕BC的解析式为y=-(1+![]() )x+4
)x+4

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案







