Question

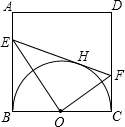
已知：如图，正方形ABCD中，AC为对角线，AE=CF．
（1）请问△AED与△CFB全等吗？请说明理由；
（2）连接EB，FD，那么四边形BFDE是菱形吗？请说明理由．

Answer 1

证明：（1）△AED与△CFB全等；
∵四边形ABCD是正方形，
∴AD=BC，∠DAC=∠BCA=45°；
又∵AE=CF，
∴△AED≌△CFB．（SAS）

（2）四边形BFDE是菱形；
证明：连接BD，交AC于O；
∵四边形ABCD是正方形，
∴AC⊥BD，且OB=OD，OA=OC；
∵AE=CF，
∴OA-AE=OC-CF，即OE=OF；
∴EF、BD互相垂直平分；
故四边形BFDE是菱形．
分析：（1）由于四边形ABCD是正方形，可得出的条件有：AD=BC，∠DAC=∠BCF=45°；又已知AE=CF，根据SAS即可证得两三角形全等．
（2）连接BD，证BD与EF互相垂直平分即可．
点评：本题主要考查了全等三角形的判定、正方形的性质以及菱形的判别方法．
菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：
①定义；
②四边相等；
③对角线互相垂直平分．
具体选择哪种方法需要根据已知条件来确定．