题目内容
已知:如图,点P是线段AB上的动点,分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD,AD和BC交于点M.
(1)当△APC和△BPD面积之和最小时,直接写出AP : PB的值和∠AMC的度数;
(2)将点P在线段AB上随意固定,再把△BPD按顺时针方向绕点P旋转一个角度α,当α<60°时,旋转过程中,∠AMC的度数是否发生变化?证明你的结论.
(3)在第(2)小题给出的旋转过程中,若限定60°<α<120°,∠AMC的大小是否会发生变化?若变化,请写出∠AMC的度数变化范围;若不变化,请写出∠AMC的度数.
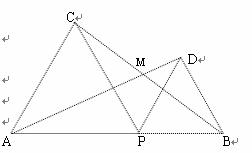
⑴ 1,60°
⑵ 不变化.
证明:如图,点E在AP的延长线上,
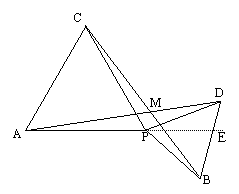 ∠BPE=α<60°.(只要画出了符合题意的图形即可得分)
∠BPE=α<60°.(只要画出了符合题意的图形即可得分)
∵∠BPC=∠CPD+60°,
∠DPA=∠CPD+60°,
∴∠BPC=∠DPA.
在△BPC和△DPA中,
又∵BP=DP,PC=PA,
∴△BPC≌△DPA.
∴∠BCP=∠DAP.
∴∠AMC=180°-∠MCP-∠PCA-∠MAC
= 120°-∠BCP -∠MAC
=120°-(∠DAP+∠MAC)-∠PCA
=120°-∠PAC
= 60°,且与α的大小无关.
⑶ 不变化,60°

练习册系列答案
相关题目
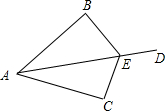 已知:如图,点E是AD上一点,AB=AC,如果AD是∠BAC的平分线.求证:EA是∠BEC的平分线.
已知:如图,点E是AD上一点,AB=AC,如果AD是∠BAC的平分线.求证:EA是∠BEC的平分线. 9、已知:如图,点C是∠AOB的角平分线的一点,CD∥OA交OB于D,CE⊥OA于E,且∠COA=15°,CE=4cm,那么CD=
9、已知:如图,点C是∠AOB的角平分线的一点,CD∥OA交OB于D,CE⊥OA于E,且∠COA=15°,CE=4cm,那么CD= 已知:如图,点O是△ABC的重心,连接AO并延长交BC于点D,则下列命题中正确的是( )
已知:如图,点O是△ABC的重心,连接AO并延长交BC于点D,则下列命题中正确的是( ) 已知,如图,点D是△ABC的两外角平分线的交点,下列说法:
已知,如图,点D是△ABC的两外角平分线的交点,下列说法: 已知:如图,点E是AD上一点,BE=CE,如果∠BEA=∠CEA.
已知:如图,点E是AD上一点,BE=CE,如果∠BEA=∠CEA.