题目内容
【题目】如图，在
中，
，
是
的一条角平分线.点
、
、
分别在、
、
上，且四边形
是正方形.
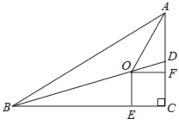
（1）求证：点在
的平分线上；
（2）若
，
，且正方形的面积为4，求
的面积.
【答案】（1）证明见解析；（2）13.
【解析】
（1）过点O作OM⊥AB，由正方形的性质可得OE=OF，OE⊥BC，OF⊥AC，根据角平分线上的点到角两边距离相等可得OM=OG，所以OM=OF，于是根据角平分线的判定定理可得点O在∠BAC的平分线上；
（2）由勾股定理得AB的长，根据正方形的面积可求OE的长，于是可得OM的长，根据三角形的面积计算公式可求.
解：（1）证明：过点O作OM⊥AB，
∵四边形OECF是正方形，
∴OE=OF，∠OEC=∠OFC =90°，
∴OE⊥BC，OF⊥AC,
∵BD是∠ABC的一条角平分线，OM⊥AB,
∴OE=OM，
∴OF=OM，
∴点O在∠BAC的平分线上；
（2）∵
，
，
，
∴在Rt△ABC中，根据勾股定理
,
∵正方形
的面积为4，
∴OM=OE=2，
∴
练习册系列答案
相关题目
【题目】为了提高学生书写汉字的能力，增强保护汉子的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每正确听写出一个汉字得1分，本次决赛，学生成绩为
（分），且
，将其按分数段分为五组，绘制出以下不完整表格：
组别 | 成绩 | 频数（人数） | 频率 |
一 |
| 2 | 0.04 |
二 |
| 10 | 0.2 |
三 |
| 14 | b |
四 |
| a | 0.32 |
五 |
| 8 | 0.16 |
请根据表格提供的信息，解答以下问题：
（1）本次决赛共有 名学生参加；
（2）直接写出表中a= ,b= ;
（3）请补全下面相应的频数分布直方图；
（4）若决赛成绩不低于80分为优秀，则本次大赛的优秀率为 。
