ÌâÄ¿ÄÚÈÝ
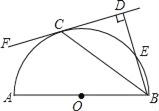
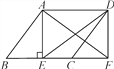
¡ŸÌâÄ¿¡¿ÈçÍŒ1£¬ÔÚËıßÐÎABCDÖУ¬AB=AD. ¡ÏB+¡ÏADC=180¡ã£¬µãE£¬F·Ö±ðÔÚËıßÐÎABCDµÄ±ßBC£¬CDÉÏ£¬¡ÏEAF=![]() ¡ÏBAD£¬Á¬œÓEF£¬ÊÔ²ÂÏëEF£¬BE£¬DFÖ®ŒäµÄÊýÁ¿¹Øϵ.
¡ÏBAD£¬Á¬œÓEF£¬ÊÔ²ÂÏëEF£¬BE£¬DFÖ®ŒäµÄÊýÁ¿¹Øϵ.

͌1 ͌2 ͌3
(1)ˌ·ÊáÀí
œ«¡÷ABEÈƵãAÄæʱÕëÐýתÖÁ¡÷ADG£¬Ê¹ABÓëADÖغÏ.ÓÉ¡ÏB+¡ÏADC=180¡ã£¬µÃ¡ÏFDG=180¡ã£¬ŒŽµãF£¬D£¬GÈýµã¹²Ïß. Ò×Ö€¡÷AFG![]() £¬¹ÊEF£¬BE£¬DFÖ®ŒäµÄÊýÁ¿¹ØϵΪ £»
£¬¹ÊEF£¬BE£¬DFÖ®ŒäµÄÊýÁ¿¹ØϵΪ £»
(2)Àà±ÈÒýÉê
ÈçÍŒ2£¬ÔÚÍŒ1µÄÌõŒþÏ£¬ÈôµãE£¬FÓÉÔÀŽµÄλÖ÷ֱð±äµœËıßÐÎABCDµÄ±ßCB£¬DCµÄÑÓ³€ÏßÉÏ£¬¡ÏEAF=![]() ¡ÏBAD£¬Á¬œÓEF£¬ÊÔ²ÂÏëEF£¬BE£¬DFÖ®ŒäµÄÊýÁ¿¹Øϵ£¬²¢žø³öÖ€Ã÷.
¡ÏBAD£¬Á¬œÓEF£¬ÊÔ²ÂÏëEF£¬BE£¬DFÖ®ŒäµÄÊýÁ¿¹Øϵ£¬²¢žø³öÖ€Ã÷.
(3)ÁªÏëÍØÕ¹
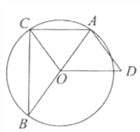
ÈçÍŒ3£¬ÔÚ¡÷ABCÖУ¬¡ÏBAC=90¡ã£¬AB=AC£¬µãD£¬EŸùÔÚ±ßBCÉÏ£¬ÇÒ¡ÏDAE=45¡ã. ÈôBD=1£¬EC=2£¬ÔòDEµÄ³€Îª .
¡ŸŽð°ž¡¿£š1£©¡÷AFE. EF=BE+DF.£š2£©BF=DF-BE£¬ÀíÓÉŒûœâÎö£»£š3£©![]()
¡ŸœâÎö¡¿ÊÔÌâ·ÖÎö£º£š1£©ÏÈžùŸÝÐýתµÃ£º ![]() ŒÆËã
ŒÆËã![]() ŒŽµã
ŒŽµã![]() ¹²Ïߣ¬ÔÙžùŸÝSASÖ€Ã÷¡÷AFE¡Õ¡÷AFG£¬µÃEF=FG£¬¿ÉµÃœáÂÛEF=DF+DG=DF+AE£»
¹²Ïߣ¬ÔÙžùŸÝSASÖ€Ã÷¡÷AFE¡Õ¡÷AFG£¬µÃEF=FG£¬¿ÉµÃœáÂÛEF=DF+DG=DF+AE£»
£š2£©ÈçÍŒ2£¬Í¬Àí×÷žšÖúÏߣº°Ñ¡÷ABEÈƵãAÄæʱÕëÐýת![]() ÖÁ¡÷ADG£¬Ö€Ã÷¡÷EAF¡Õ¡÷GAF£¬µÃEF=FG£¬ËùÒÔEF=DFDG=DFBE;
ÖÁ¡÷ADG£¬Ö€Ã÷¡÷EAF¡Õ¡÷GAF£¬µÃEF=FG£¬ËùÒÔEF=DFDG=DFBE;
£š3£©ÈçÍŒ3£¬Í¬Àí×÷žšÖúÏߣº°Ñ¡÷ABDÈƵãAÄæʱÕëÐýת![]() ÖÁ¡÷ACG£¬Ö€Ã÷¡÷AED¡Õ¡÷AEG£¬µÃ
ÖÁ¡÷ACG£¬Ö€Ã÷¡÷AED¡Õ¡÷AEG£¬µÃ![]() £¬ÏÈÓɹŽ¹É¶šÀíÇó
£¬ÏÈÓɹŽ¹É¶šÀíÇó![]() µÄ³€£¬ŽÓ¶øµÃœáÂÛ£®
µÄ³€£¬ŽÓ¶øµÃœáÂÛ£®
ÊÔÌâœâÎö£º(1)ˌ·ÊáÀí£º
ÈçÍŒ1,°Ñ¡÷ABEÈƵãAÄæʱÕëÐýת![]() ÖÁ¡÷ADG£¬¿ÉʹABÓëADÖغϣ¬ŒŽAB=AD£¬
ÖÁ¡÷ADG£¬¿ÉʹABÓëADÖغϣ¬ŒŽAB=AD£¬
ÓÉÐýתµÃ£º¡ÏADG=¡ÏA=![]() £¬BE=DG£¬¡ÏDAG=¡ÏBAE£¬AE=AG£¬
£¬BE=DG£¬¡ÏDAG=¡ÏBAE£¬AE=AG£¬
¡à¡ÏFDG=¡ÏADF+¡ÏADG=![]() +
+![]() =
=![]() £¬
£¬
ŒŽµãF. D.G¹²Ïߣ¬
¡ßËıßÐÎABCDΪŸØÐΣ¬
¡à¡ÏBAD=![]() £¬
£¬
¡ß¡ÏEAF=![]() £¬
£¬
¡à![]()
¡à![]()
¡à![]()
ÔÚ¡÷AFEºÍ¡÷AFGÖУ¬
¡ß
¡à¡÷AFE¡Õ¡÷AFG(SAS)£¬
¡àEF=FG£¬
¡àEF=DF+DG=DF+AE
¹ÊŽð°žÎª£º¡÷AFE£¬EF=DF+AE£»
(2)Àà±ÈÒýÉ꣺
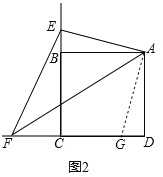
ÈçÍŒ2£¬EF=DFBE£¬ÀíÓÉÊÇ£º
°Ñ¡÷ABEÈƵãAÄæʱÕëÐýת![]() ÖÁ¡÷ADG£¬¿ÉʹABÓëADÖغϣ¬ÔòGÔÚDCÉÏ£¬
ÖÁ¡÷ADG£¬¿ÉʹABÓëADÖغϣ¬ÔòGÔÚDCÉÏ£¬
ÓÉÐýתµÃ£ºBE=DG£¬¡ÏDAG=¡ÏBAE£¬AE=AG£¬
¡ß¡ÏBAD=![]() £¬
£¬
¡à¡ÏBAE+¡ÏBAG=![]() £¬
£¬
¡ß¡ÏEAF=![]() £¬
£¬
¡à¡ÏFAG=![]()
![]() =
=![]() £¬
£¬
¡à¡ÏEAF=¡ÏFAG=![]() £¬
£¬
ÔÚ¡÷EAFºÍ¡÷GAFÖУ¬
¡ß
¡à¡÷EAF¡Õ¡÷GAF(SAS)£¬
¡àEF=FG£¬
¡àEF=DFDG=DFBE;
(3)ÁªÏëÍØÕ¹£º
ÈçÍŒ3,°Ñ¡÷ABDÈƵãAÄæʱÕëÐýת![]() ÖÁ¡÷ACG£¬¿ÉʹABÓëACÖغϣ¬Á¬œÓEG£¬
ÖÁ¡÷ACG£¬¿ÉʹABÓëACÖغϣ¬Á¬œÓEG£¬
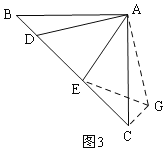
ÓÉÐýתµÃ£ºAD=AG£¬¡ÏBAD=¡ÏCAG£¬BD=CG£¬
¡ß¡ÏBAC=![]() £¬AB=AC£¬
£¬AB=AC£¬
¡à¡ÏB=¡ÏACB=![]() £¬
£¬
¡à¡ÏACG=¡ÏB=![]() £¬
£¬
¡à¡ÏBCG=¡ÏACB+¡ÏACG=![]() +
+![]() =
=![]() £¬
£¬
¡ßEC=2£¬CG=BD=1£¬
ÓɹŽ¹É¶šÀíµÃ£º ![]()
¡ß¡ÏBAD=¡ÏCAG,¡ÏBAC=
¡à¡ÏDAG=![]() £¬
£¬
¡ß¡ÏBAD+¡ÏEAC=![]() £¬
£¬
¡à¡ÏCAG+¡ÏEAC=![]() =¡ÏEAG£¬
=¡ÏEAG£¬
¡à¡ÏDAE=![]() £¬
£¬
¡à¡ÏDAE=¡ÏEAG=![]() £¬
£¬
¡ßAE=AE£¬
¡à¡÷AED¡Õ¡÷AEG£¬
¡à![]()