题目内容
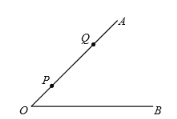
【题目】如图,![]() ,点
,点![]() 、
、![]() 都在射线
都在射线![]() 上,
上,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上的一个动点,过
上的一个动点,过![]() 、
、![]() 、
、![]() 三点作圆,当该圆与
三点作圆,当该圆与![]() 相切时,其半径的长为__________.
相切时,其半径的长为__________.
【答案】![]()
【解析】
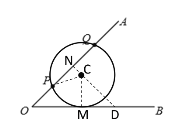
圆C过点P、Q,且与![]() 相切于点M,连接CM,CP,过点C作CN⊥PQ于N并反向延长,交OB于D,根据等腰直角三角形的性质和垂径定理,即可求出ON、ND、PN,设圆C的半径为r,再根据等腰直角三角形的性质即可用r表示出CD、NC,最后根据勾股定理列方程即可求出r.
相切于点M,连接CM,CP,过点C作CN⊥PQ于N并反向延长,交OB于D,根据等腰直角三角形的性质和垂径定理,即可求出ON、ND、PN,设圆C的半径为r,再根据等腰直角三角形的性质即可用r表示出CD、NC,最后根据勾股定理列方程即可求出r.
解:如图所示,圆C过点P、Q,且与![]() 相切于点M,连接CM,CP,过点C作CN⊥PQ于N并反向延长,交OB于D
相切于点M,连接CM,CP,过点C作CN⊥PQ于N并反向延长,交OB于D
∵![]() ,
,![]() ,
,
∴PQ=OQ-OP=4
根据垂径定理,PN=![]()
∴ON=PN+OP=4
在Rt△OND中,∠O=45°
∴ON=ND=4,∠NDO=∠O=45°,OD=![]()
设圆C的半径为r,即CM=CP=r
∵圆C与![]() 相切于点M,
相切于点M,
∴∠CMD=90°
∴△CMD为等腰直角三角形
∴CM=DM=r,CD=![]()
∴NC=ND-CD=4-![]()
根据勾股定理可得:NC2+PN2=CP2
即![]()
解得:![]() (此时DM>OD,点M不在射线OB上,故舍去)
(此时DM>OD,点M不在射线OB上,故舍去)
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目