��Ŀ����
����Ŀ��ʱ�����ij�̳���Ӫ��ijƷ�������6�·ݵ����۶�Ϊ20000Ԫ��7�·���Ϊ��������˳����ۣ��̳��Ѹ�Ʒ������ۼ�����20%�������������50����ʹ�����۶������2000Ԫ��
��1����6�·ݸ�Ʒ����������۵��ۣ�
��2����6�·����۸�Ʒ���������8000Ԫ��8�·��̳�Ϊӭ����Сѧ��ѧ����������������6���ۼ۵Ļ�����һ�ɴ�������ۣ����ɱ�����5%������������Ϊ���ٸ������ܱ�֤8�·ݵ������6�·ݵ�������������6.25%��
���𰸡���1��6�·ݸ�Ʒ����������۵���Ϊ100Ԫ����2����������Ϊ500��ʱ�����ܱ�֤8�·ݵ������6�·ݵ�������������6.25%��
��������
��1����6�·ݸ�Ʒ����������۵���ΪxԪ����7�·ݸ�Ʒ����������۵���Ϊ��1+20%��xԪ�������������ܼۡµ��۽��7�·ݵ�����������6�·ݼ�����50�������ɵó�����x�ķ�ʽ���̣���֮������ɵó����ۣ�
��2�������������ܼۡµ��ۿ����6�·ݸ�Ʒ�������������������Ͻ��ۣ���6�·ݸ�Ʒ����������۶�����������������6�·ݸ�Ʒ������Ľ��ۣ���������������������������������8�·ݵ������6�·ݵ�������������6.25%�����ɵó�����y��һԪһ�β���ʽ����֮ȡ���е���Сֵ���ɵó����ۣ�
�⣺��1����6�·ݸ�Ʒ����������۵���ΪxԪ����7�·ݸ�Ʒ����������۵���Ϊ��1+20%��xԪ��
�����⣬�ã�![]() ��
��
��ã�x��100��
�����飬x��100��ԭ���̵Ľ⣬�ҷ������⣮
��6�·ݸ�Ʒ����������۵���Ϊ100Ԫ��
��2��6�·ݸ�Ʒ���������������Ϊ20000��100��200��������
6�·ݸ�Ʒ������Ľ���Ϊ��20000��8000����200��60��Ԫ����
��8�·ݸ�Ʒ���������������Ϊy����
�����⣬�ã�[100��0.8����1+5%����60]y��8000����1+6.25%����
��ã�y��500��
����������Ϊ500��ʱ�����ܱ�֤8�·ݵ������6�·ݵ�������������6.25%��

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
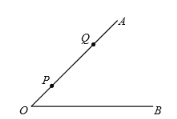
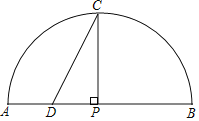
�����ܿ����ϵ�д�����Ŀ����ͼ��P��![]() ������AB��һ���㣬����P��PC��AB��
������AB��һ���㣬����P��PC��AB��![]() �ڵ�C��ȡAP�е�D������CD����֪AB=6cm����A��P�����ľ���Ϊxcm��C��D�����ľ���Ϊycm��������P���A�غ�ʱ��y��ֵΪ0������P���B�غ�ʱ��y��ֵΪ3��
�ڵ�C��ȡAP�е�D������CD����֪AB=6cm����A��P�����ľ���Ϊxcm��C��D�����ľ���Ϊycm��������P���A�غ�ʱ��y��ֵΪ0������P���B�غ�ʱ��y��ֵΪ3��
С������ѧϰ�����ľ��飬�Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С����̽�����̣��벹��������
��1��ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ���ֵ�����±���
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.2 | 3.2 | 3.4 | 3.3 | 3 |
��2������ƽ��ֱ������ϵ�������ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
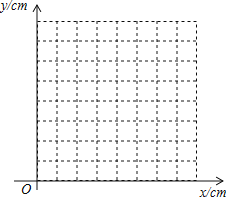
��3������������ĺ���ͼ������⣺����C=30��ʱ��AP�ij���ԼΪ cm��
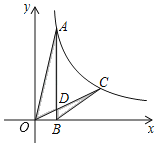
����Ŀ����֪���κ���![]() ��
��![]() ��
��![]() �IJ��ֶ�Ӧֵ�����
�IJ��ֶ�Ӧֵ�����
|
|
|
|
|
|
|
|
|
|
|
|
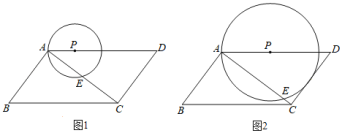
���н��ۣ��������ߵĿ������ϣ��������ߵĶԳ���Ϊֱ��![]() ������
������![]() ʱ��
ʱ��![]() ������������
������������![]() ������������ľ�����
������������ľ�����![]() ������
������![]() �������������㣬��
�������������㣬��![]() ����
����![]() . ������ȷ�ĸ�����( )
. ������ȷ�ĸ�����( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()