题目内容
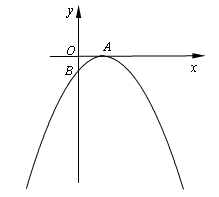
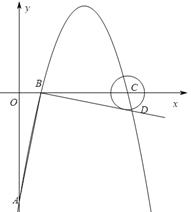
如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,﹣2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.

(1)求此抛物线的解析式;
(2)求证:AO=AM;
(3)探究:
①当k=0时,直线y=kx与x轴重合,求出此时 的值;
的值;
②试说明无论k取何值, 的值都等于同一个常数.
的值都等于同一个常数.

(1)求此抛物线的解析式;
(2)求证:AO=AM;
(3)探究:
①当k=0时,直线y=kx与x轴重合,求出此时
 的值;
的值;②试说明无论k取何值,
 的值都等于同一个常数.
的值都等于同一个常数.解:(1)∵抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1),
∴ ,解得
,解得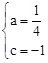 。
。
∴抛物线的解析式为y=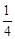 x2﹣1。
x2﹣1。
(2)证明:设点A的坐标为(m,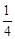 m2﹣1),
m2﹣1),
则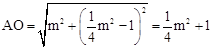 。
。
∵直线l过点E(0,﹣2)且平行于x轴,∴点M的纵坐标为﹣2。
∴AM=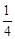 m2﹣1﹣(﹣2)=
m2﹣1﹣(﹣2)=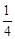 m2+1。
m2+1。
∴AO=AM。
(3)①k=0时,直线y=kx与x轴重合,点A、B在x轴上,
∴AM=BN=0﹣(﹣2)=2,
∴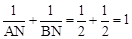 。
。
②k取任何值时,设点A(x1,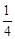 x12﹣1),B(x2,
x12﹣1),B(x2,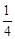 x22﹣1),
x22﹣1),
则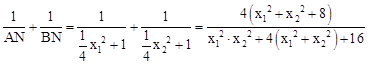 。
。
联立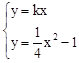 ,消掉y得,x2﹣4kx﹣4=0,
,消掉y得,x2﹣4kx﹣4=0,
由根与系数的关系得,x1+x2=4k,x1•x2=﹣4,
∴x12+x22=(x1+x2)2﹣2x1•x2=16k2+8,x12•x22=16。
∴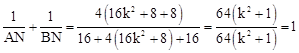 。
。
∴无论k取何值, 的值都等于同一个常数1。
的值都等于同一个常数1。
∴
 ,解得
,解得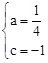 。
。∴抛物线的解析式为y=
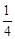 x2﹣1。
x2﹣1。(2)证明:设点A的坐标为(m,
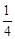 m2﹣1),
m2﹣1),则
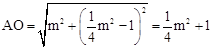 。
。∵直线l过点E(0,﹣2)且平行于x轴,∴点M的纵坐标为﹣2。
∴AM=
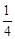 m2﹣1﹣(﹣2)=
m2﹣1﹣(﹣2)=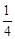 m2+1。
m2+1。∴AO=AM。
(3)①k=0时,直线y=kx与x轴重合,点A、B在x轴上,
∴AM=BN=0﹣(﹣2)=2,
∴
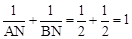 。
。②k取任何值时,设点A(x1,
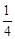 x12﹣1),B(x2,
x12﹣1),B(x2,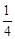 x22﹣1),
x22﹣1),则
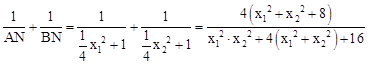 。
。联立
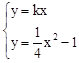 ,消掉y得,x2﹣4kx﹣4=0,
,消掉y得,x2﹣4kx﹣4=0,由根与系数的关系得,x1+x2=4k,x1•x2=﹣4,
∴x12+x22=(x1+x2)2﹣2x1•x2=16k2+8,x12•x22=16。
∴
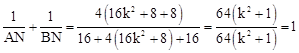 。
。∴无论k取何值,
 的值都等于同一个常数1。
的值都等于同一个常数1。试题分析:(1)把点C、D的坐标代入抛物线解析式求出a、c,即可得解。
(2)根据抛物线解析式设出点A的坐标,然后求出AO、AM的长,即可得证。
(3)①k=0时,求出AM、BN的长,然后代入
 计算即可得解;
计算即可得解;②设点A(x1,
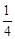 x12﹣1),B(x2,
x12﹣1),B(x2, x22﹣1),然后表示出
x22﹣1),然后表示出 ,再联立抛物线与直线解析式,消掉未知数y得到关于x的一元二次方程,利用根与系数的关系表示出x1+x2,x1•2,并求出x12+x22,x12•x22,然后代入进行计算即可得解。
,再联立抛物线与直线解析式,消掉未知数y得到关于x的一元二次方程,利用根与系数的关系表示出x1+x2,x1•2,并求出x12+x22,x12•x22,然后代入进行计算即可得解。
练习册系列答案
相关题目

 .
.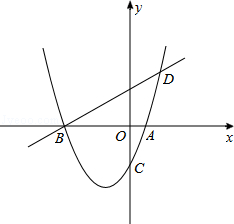
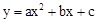 的顶点A(2,0),与y轴的交点为B(0,-1).
的顶点A(2,0),与y轴的交点为B(0,-1).